Modelle, nach denen wir Entscheidungen treffen, werden in meinen Augen oft zu wenig bis gar nicht hinterfragt und validiert. Obwohl das so wichtig wäre, denn nicht passfähige Modelle erzeugen nicht passfähige Entscheidungen und damit nicht passfähige Handlungen. Genau um diesen Fakt soll es in diesem Beitrag gehen, und zwar im Kontext der Ökonomie. Denn einige Gesetzmäßigkeiten, die in der Ökonomie vorherrschend sind und scheinbar wie Naturgesetze daher kommen, basieren auf nicht passfähigen mathematischen Modellen.
Ideen in diesem Kontext habe ich vor ein paar Jahren schon einmal im Beitrag namens Erkenntnisse der Mathematik werden falsch in die Wirtschaft portiert offenbart. Nun wurde ich auf dem diesjährigen LeanAroundTheClock 2019 wieder auf diese Problematik aufmerksam gemacht, nämlich von Stefan Röcker in der Themenbox der priomys, wo wir über NewWork diskutiert haben.
Im Rahmen dieser Diskussion warf Stefan das Buch Gier von Marc Elsberg in den Raum und erwähnte, dass in diesem Roman die mathematischen Modelle, auf denen unsere Ökonomie fußt, als nicht passfähig dargestellt werden. Da hat er mich als Mathematiker natürlich sofort gehabt. Ich habe mir am gleichen Tag das Buch bestellt und gelesen, nein verschlungen. 🙂
Elsberg deckt in diesem Buch in Romanform Fehler im mathematischen Fundament der Ökonomie auf, was letztendlich zu nicht passfähigen Entscheidungen und dann zu nicht passfähigen Handlungen führt. Hier findet man ein paar Hintergrundinformationen zum Anliegen dieses Buchprojektes.
Das Spiel
Der Autor lässt in dem Roman einen seiner Romanfiguren, Fitzroy Peel, anderen Menschen ein Spiel anbieten. In einer Kneipe schlägt er Folgendes vor. Einsatz je Spieler sind 100 Euro. Dann wird 100 Runden lang eine Münze geworfen. In jeder Runde wird bei Kopf 50% des derzeitigen Vermögens gewonnen und bei Zahl 40% verloren. Alle der angesprochenen Menschen in der Bar gehen das Spiel ein, natürlich im Gefühl des sicheren Gewinns. Wie rechnen diese Menschen? Würden Sie spielen?
Die Wahrscheinlichkeit für Kopf beträgt 50%, ebenso wie für Zahl. Wenn man nun diese Wahrscheinlichkeiten mit den Gewinn- und Verlustchancen kombiniert, erhält man den Erwartungswert.
Erwartungswert = 50% * (1 + 50%) + 50% * (1 – 40%) = 105%.
Bei dieser Rechnung steigt also das jeweilige Vermögen je Runde um 5%. Bei 100 Euro als Startvermögen beträgt der statistische Erwartungswert für das Gesamtvermögen nach 100 Runden also 13.150,13 Euro. Nach dieser Rechnung ist die Entscheidung, ob man das Spiel eingehen sollte oder nicht, klar. Auf jeden Fall spielen. Aber, ist die Rechnung richtig? Was wurde hier außer Acht gelassen?
Ergodizität
Für die Überprüfung der Passfähigkeit dieser Berechnung führe ich einen Begriff ein, die Ergodizität. Ergodizität ist eine Eigenschaft dynamischer Systeme. Ich zitiere Wikipedia.
Die Ergodizität bezieht sich auf das mittlere Verhalten eines Systems. Ein solches System wird durch eine Musterfunktion beschrieben, die die zeitliche Entwicklung des Systems abhängig von seinem aktuellen Zustand bestimmt. Man kann nun auf zweierlei Arten mitteln:
- Man kann die Entwicklung über einen langen Zeitraum verfolgen und über diese Zeit mitteln, also den Zeitmittelwert bilden, oder
- Man kann alle möglichen Zustände betrachten und über diese mitteln, also das Scharmittel (Ensemblemittel) bilden.
Streng ergodisch wird ein System dann genannt, wenn die Zeitmittel und Scharmittel mit der Wahrscheinlichkeit eins zum gleichen Ergebnis führen. Anschaulich bedeutet das, dass während der Entwicklung des Systems alle möglichen Zustände erreicht werden, der Zustandsraum also mit der Zeit vollständig ausgefüllt wird. Das bedeutet insbesondere, dass bei solchen Systemen der Erwartungswert nicht vom Anfangszustand abhängig ist.
Reflektieren wir diese Erkenntnis mal auf das Spiel. Das reine Werfen der Münze ist streng ergodisch. Nach 100 Würfen nähert sich das Vorkommen von „Kopf“ und „Zahl“ der 50% an. Alle möglichen Zustände, genau 2, „Kopf“ und „Zahl“, werden vollständig eingenommen. Der Erwartungswert 50% für „Kopf“ und „Zahl“ ist nicht abhängig davon, ob beim ersten Wurf „Kopf“ oder „Zahl“ geworfen wurde. Man könnte hier auch von statistischer Unabhängigkeit sprechen. Hier ist der Ensemblemittelwert zur Beschreibung dieses Systems passfähig. Was passiert aber bei der Hinzunahme der monetären Bewertung?
Spielen wir der Anschaulichkeit halber mal nur 2 Runden. In der 1. Runde fällt „Kopf“. Dann erhöht sich das Vermögen auf 150 Euro (plus 50%). In der 2. Runde fällt „Zahl“. Das Vermögen verringert sich auf 90 Euro (minus 40%). In der entgegengesetzten Reihenfolge, also erst „Zahl“ und dann „Kopf“, kommt man ebenfalls auf 90 Euro. Man erhält nach 2 Runden stets 90 Euro, obwohl „Kopf“ und „Zahl“ in gleicher Anzahl vorkommen. Man besitzt damit nach 2 Runden 10 Euro weniger als zum Spielbeginn. Hätten wir das vermutet? Die Gewinnrate ist höher als die Verlustrate und ich habe trotzdem weniger Vermögen. Wie kommt das?
Der Grund dafür ist die Nicht-Ergodizität des Systems, was dazu führt, dass der Ensemblemittelwert nicht mehr passfähig ist. Nun sollte man den anderen Mittelwert zu Rate ziehen, den Zeitmittelwert, da nun der so genannte Zinseszinseffekt ins Spiel kommt. Mit jeder Runde ändert sich die Berechnungsbasis. Es liegt keine statistische Unabhängigkeit mehr vor, da das Vermögen in Runde (n-1) entscheidend ist für das Vermögen in Runde n. Das war beim reinen Werfen der Münze nicht der Fall.
Menschen die eine Teilnahme am Spiel nach dem Zeitmittelwert bewerten, welcher für diese Situation passfähig ist, kommen zu der Entscheidung nicht zu spielen. Wir sehen also, dass unterschiedliche Modelle zu unterschiedlichen Entscheidungen führen. Das kann verheerend sein. Ich habe das Spiel in Excel simuliert und folgende Ergebnisse erhalten, die diese angesprochene Dynamik verdeutlichen. Wer die Datei haben mag, kann mich gerne anschreiben. Ich sende das Modell dann zu.
Was erkennt man in der Graphik, in der 4 verschiedene Simulationsläufe abgetragen sind? Wenn der sehr unwahrscheinliche Effekt auftritt, dass nach 100 Runden „Kopf“ um ein Vielfaches mehr als „Zahl“ auftritt, hat man eine Chance nach 100 Runden sein Vermögen zu vermehren. Dieser Effekt wird aber je mehr Runden man spielt immer unwahrscheinlicher. Deshalb geht die Wahrscheinlichkeit, dass man nach 200 Runden sein Vermögen vermehrt hat, hat gegen Null, da der Ensemblemittelwert 50% des Vorkommens von „Kopf“ und „Zahl“ immer mehr Realität wird. Die Berechnung, dass man je Runde sein Vermögen um 5% steigert, ist falsch.
Nach welcher Formel lässt sich denn nun der Zeitmittelwert berechnen? Wir haben oben 2 Runden kurz angedacht. Das ergibt also den Faktor 1,5 (50% gewinnen) * 0,6 (40% verlieren) = 0,9 (Nach 2 Runden: 100 Euro * 0,9 = 90 Euro). Wenn 100 Runden gespielt werden sollen, muss man diesen Faktor mit 50 potenzieren, da dieser Faktor für jeweils 2 Runden gilt. Damit kommt man auf die Zahl 0,005153775 (=0,950). Und diese Zahl muss man nun mit 100 multiplizieren (100 Euro Startwert). Man erhält also 0,515377521 Euro, also ca. 50 Cent.
Nimmt man den Zeitmittelwert als Basis für die Berechnung erhält man nach 100 Runden rund 50 Cent und nicht 13.150,13 Euro, wie nach dem Ensemblemittelwert. Krass, dieser Unterschied, oder? Mit dieser neuen Berechnung kommt man natürlich zum Ergebnis eher nicht zu spielen. Dieses Ergebnis erkennt man in den Ergebnissen der Simulation auch schon eher. 2 unterschiedliche mathematische Modelle führen also zu unterschiedlichen Entscheidungen.
Übertragung auf die Ökonomie
Der Autor lässt die Romanfiguren auf unglaublich spannende und einleuchtende Art und Weise auf Grundlage der Erkenntnis über die Unterschiede der beiden Mittelwerte weitere Überlegungen anstellen.
Unsere derzeitigen ökonomischen Modelle basieren auf dem Ensemblemittelwert. Das ist nicht passfähig, da dieser nur bei statistischer Unabhängigkeit anzuwenden ist, also wenn die Elemente eines Systems nicht interagieren. Komplexe Systeme, wie das ökonomische eines ist, sind aber eben aufgrund ihrer Vernetzung komplex und damit auch emergent. Das Ganze ist mehr (Das „Mehr“ verstehe ich nicht nur quantitativ, sondern vor allem auch qualitativ) als die Summe ihrer Teile. Aus dem Zusammenwirken der Elemente entstehen Eigenschaften, die aus den Elementen heraus nicht erklärbar sind.
Der Zeitmittelwert sollte in der Ökonomie Basis der Berechnungen und damit der Entscheidungen sein. Das ökonomische System ist nicht ergodisch, was relativ leicht erklärbar ist. Es werden in der Realität kaum alle möglichen Zustände im ökonomischen System eingenommen. Mit jeder Entscheidung, die man zum Zeitpunkt n trifft, werden bestimmte andere Zustände, die vor dieser Entscheidung noch wahrscheinlich waren, nun unwahrscheinlich und neue mögliche Zustände kommen hinzu. Das bedeutet, ähnlich wie bei dem Münzspiel ändert sich im ökonomischen System mit jeder getroffenen Entscheidung die Situation für kommende nachfolgende Entscheidungen und Handlungen. Die Berechnungsbasis ändert sich.
Durch diese Interaktionen der Elemente, im ökonomischen System sind das die Menschen, wird aber auch klar, dass Kooperation mehr zum Gemeinwohl beiträgt als Konkurrenz, was das Modell des Homo Oeconomicus auch ins Reich der Fabeln verweist. Unsere Welt ist durch unseren technologischen Fortschritt und die damit verbundene höhere Vernetzung eh komplexer geworden. Begegnen wir diesem Phänomen mit wenig Vernetzung (Interaktion) und damit mit weniger Kooperation und mit mehr Konkurrenz, verringern wir im jeweiligen System (z.B. Unternehmen) die Eigenkomplexität, was dazu führt, dass die Komplexität der Umwelt (z.B. Markt) schlechter zu handhaben ist (Ashbys Law). Diesen Fakt kennt man unter anderem auch aus dem Teamsport. Ein Team bestehend aus den besten Einzelspielern muss noch lange nicht gewinnen, und zwar genau dann nicht, wenn diese Einzelspieler nicht zusammen harmonieren.
Der Autor führt im Roman mit der so genannten Bauernfabel die Unterscheidung zwischen additivem (Ensemblemittelwert) und multiplikativem (Zeitmittelwert) Wachstum ein. Die Natur wächst eher multiplikativ, nicht additiv. Unsere ökonomischen Modelle basieren auf additivem Wachstum (Ensemblemittelwert), was nicht passfähig ist. Das haben wir gesehen. Man kann es sich aber auch auf andere Art und Weise leicht erklären. Wenn man nichts hat, kann man auch nicht einfach etwas generieren: 0 MAL irgendetwas bleibt Null. Das passt. 0 PLUS irgendetwas ist aber größer als 0. Das passt für die Ökonomie nicht.
Also Vorsicht beim Anwenden von Mathematik für die Berechnung von Entscheidungsbasen.
(11 Bewertung(en), Durchschnitt: 4.73 von 5)
Loading...
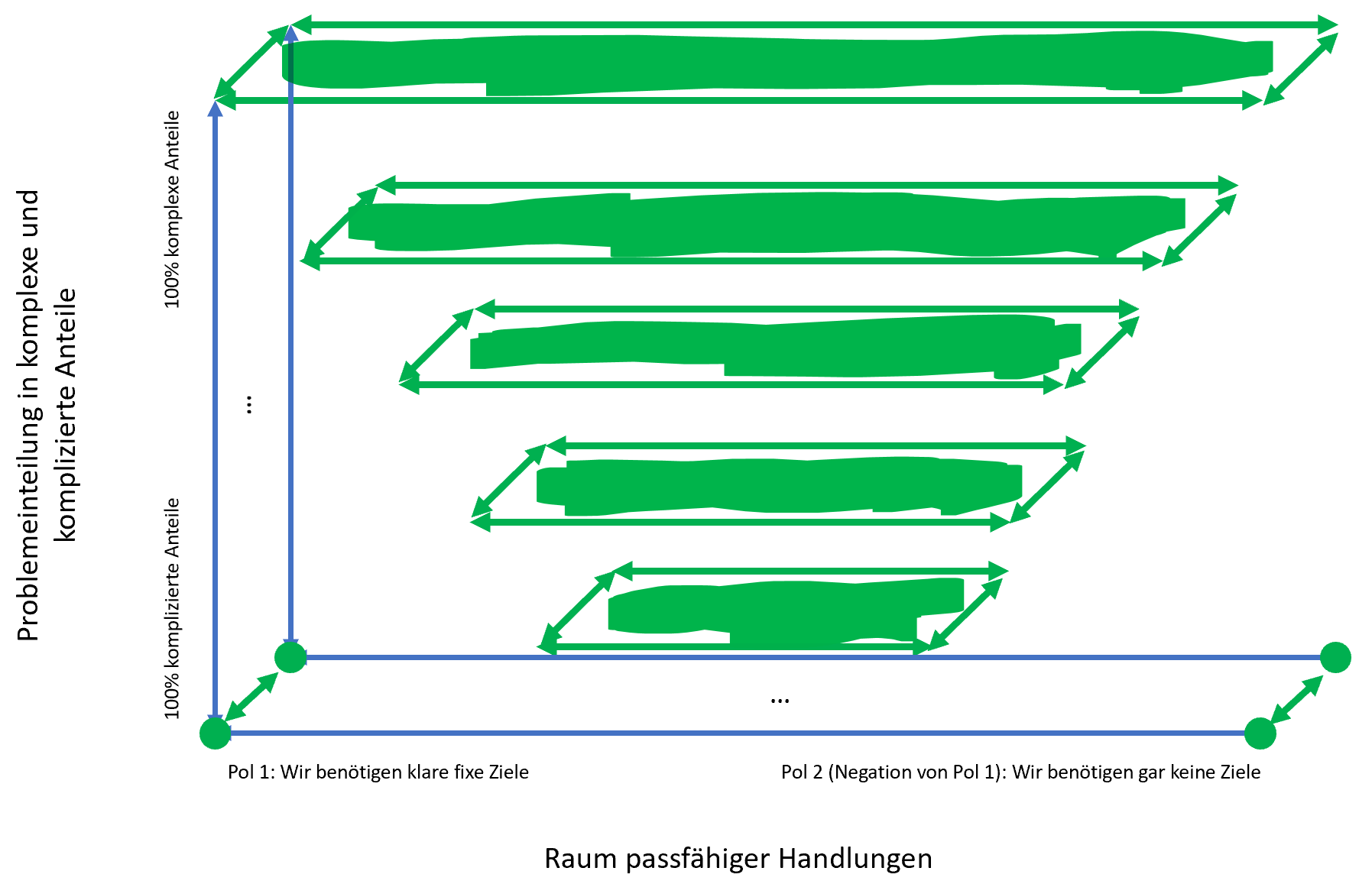
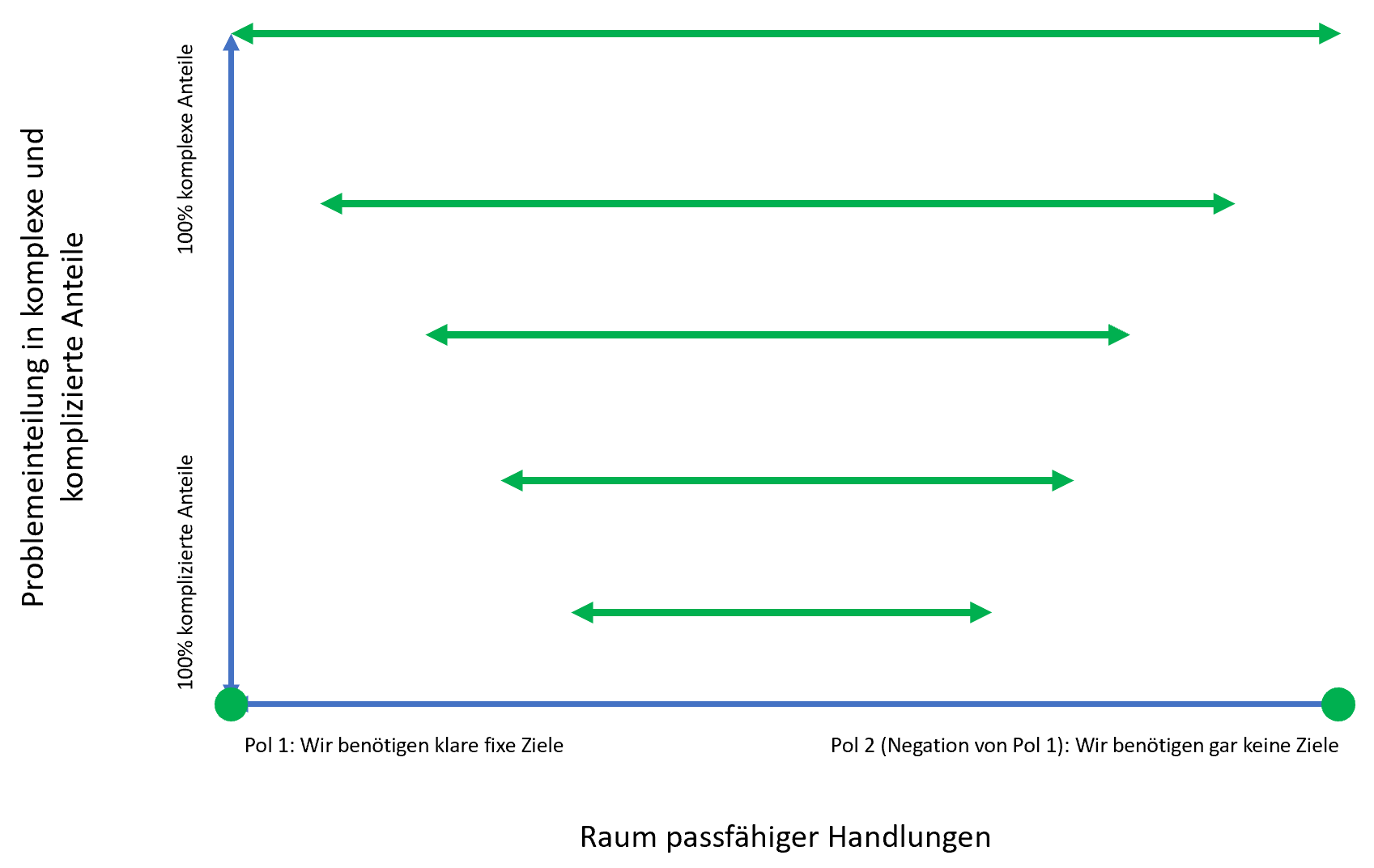Aus dem oben zugelinkten Beitrag ist ersichtlich, wie ich komplexe Probleme definiere.
(2 Bewertung(en), Durchschnitt: 3.50 von 5)
