Ich möchte illustrieren, weshalb man beim Lösen von komplexen Problemen eher “Wer?” statt “Wie?” fragen sollte.
In diesem Beitrag habe ich bereits Eigenschaften komplexer und komplizierter Probleme und Situationen dargelegt. Wichtig dabei ist zu betonen, dass ich mich beim Beschäftigen von Komplexität und Kompliziertheit nicht darauf fokussiere, wie Komplexität entsteht, sondern darauf, was komplexe Probleme, gerade im Unterschied zu komplizierten, ausmacht. Denn aus diesen Eigenschaften lassen sich passfähige Handlungen ableiten, nicht aus der Erkenntnis, wie diese Probleme entstehen.
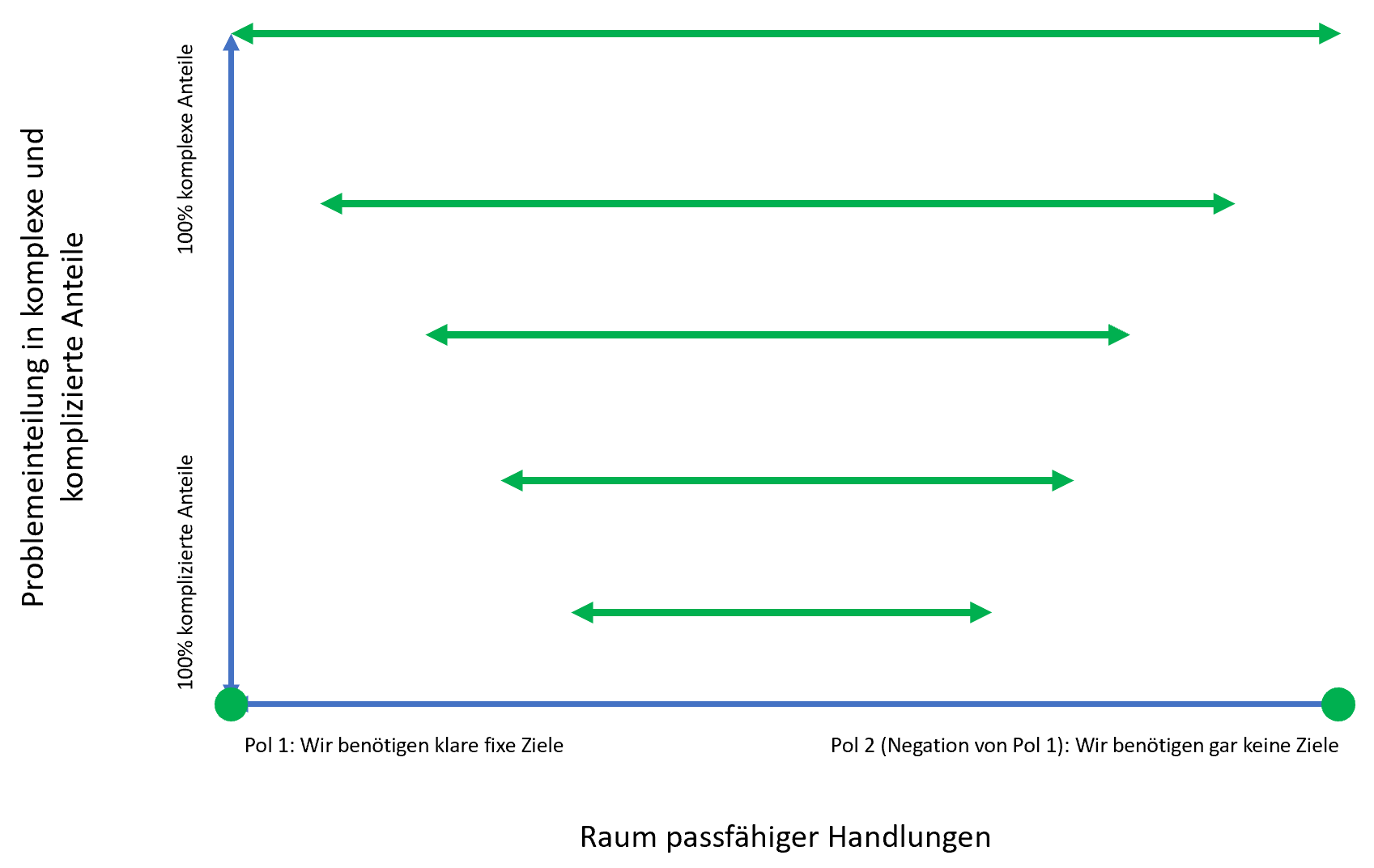
Die untere Abbildung stellt die Beziehung zwischen dem Anteil der komplexen und komplizierten Anteile an zu lösenden Problemen (y-Achse) und dem Raum passfähiger Handlungen (x-Achse) dar, allerdings nur im 1-dimensionalen Raum an passfähigen Handlungen. Dazu kommen wir gleich.
 Aus dem oben zugelinkten Beitrag ist ersichtlich, wie ich komplexe Probleme definiere.
Aus dem oben zugelinkten Beitrag ist ersichtlich, wie ich komplexe Probleme definiere.
Je mehr komplexe Anteile ein zu lösendes Problem besitzt, desto weniger handlungsleitend beschreibbar ist dieses Problem und damit die Lösung.
Genauer habe ich diese Definition in diesem Beitrag beschrieben.
Welche Erkenntnisse ziehen wir nun aus der Abbildung?
Besitzt ein Problem 100% komplizierte (handlungsleitend beschreibbare) Anteile, und damit 0% komplexe (handlungsleitend nicht beschreibbare) Anteile, so gibt es genau 2 Alternativen für eine passfähige Handlung. Diese sind auf der x-Achse mit einem grünen Punkt gekennzeichnet. Es bleibt allerdings zu betonen, dass diese Probleme wohl nur theoretisch existieren, da immer dann, wenn der Mensch in ein Problem eingreift, die komplexen Anteile größer Null sein müssen.
Je größer die komplexen Anteile eines Problems werden, desto größer wird auch der 1-dimensionale Raum an passfähigen Handlungen.
Das passt zu der Eigenschaft komplexer Probleme. Je größer die komplexen Anteile werden, desto eher zieht man mit jeder passfähigen Handlung negative Wirkungen mit. Es ist ebenfalls ersichtlich, dass, je mehr komplexe Anteile ein Problem hat, desto weniger ein Rezept zum Lösen vorliegen kann, da man immer mehr mögliche Kontexte der Zukunft in das Rezept einbauen müsste, was immer unmöglicher wird, je größer die komplexen Anteile werden.
Das einmal angewendet auf ein konkretes Beispiel. Ich nehme einen bestimmten Polstrang heraus, der in der obigen Abbildung auch dargestellt ist.
- Pol 1: Ich benötige ein konkretes fixes Ziel um erfolgreich zu sein. und
- Pol 2: Ich benötige kein Ziel, um erfolgreich zu sein. (Negation von Pol 1).
Weder der Pol 1 noch Pol 2 stellt Alternativen für passfähige Handlungen dar. Passfähige Handlungen sollten also auf diesem Strang ausbalanciert werden. Und je mehr komplexe Anteile ein Problem hat, desto größer wird dieser 1-dimensionale Raum zur Ausbalancierung, wie in der obigen Abbildung illustriert.
Möchte ich eine Uhr reparieren, ist der Raum passfähiger Handlungen kleiner, als wenn ich ein Unternehmen führen möchte. Desto eher sind also konkrete Handlungsbeschreibungen für das Reparieren einer Uhr möglich als für das Führen eines Unternehmens.
Besitzt ein Problem 100% komplexe Anteile, dann ist der 1-dimensionale Raum an passfähigen Handlungen größtmöglich. Aber auch diese Probleme sind wohl eher theoretischer Natur.
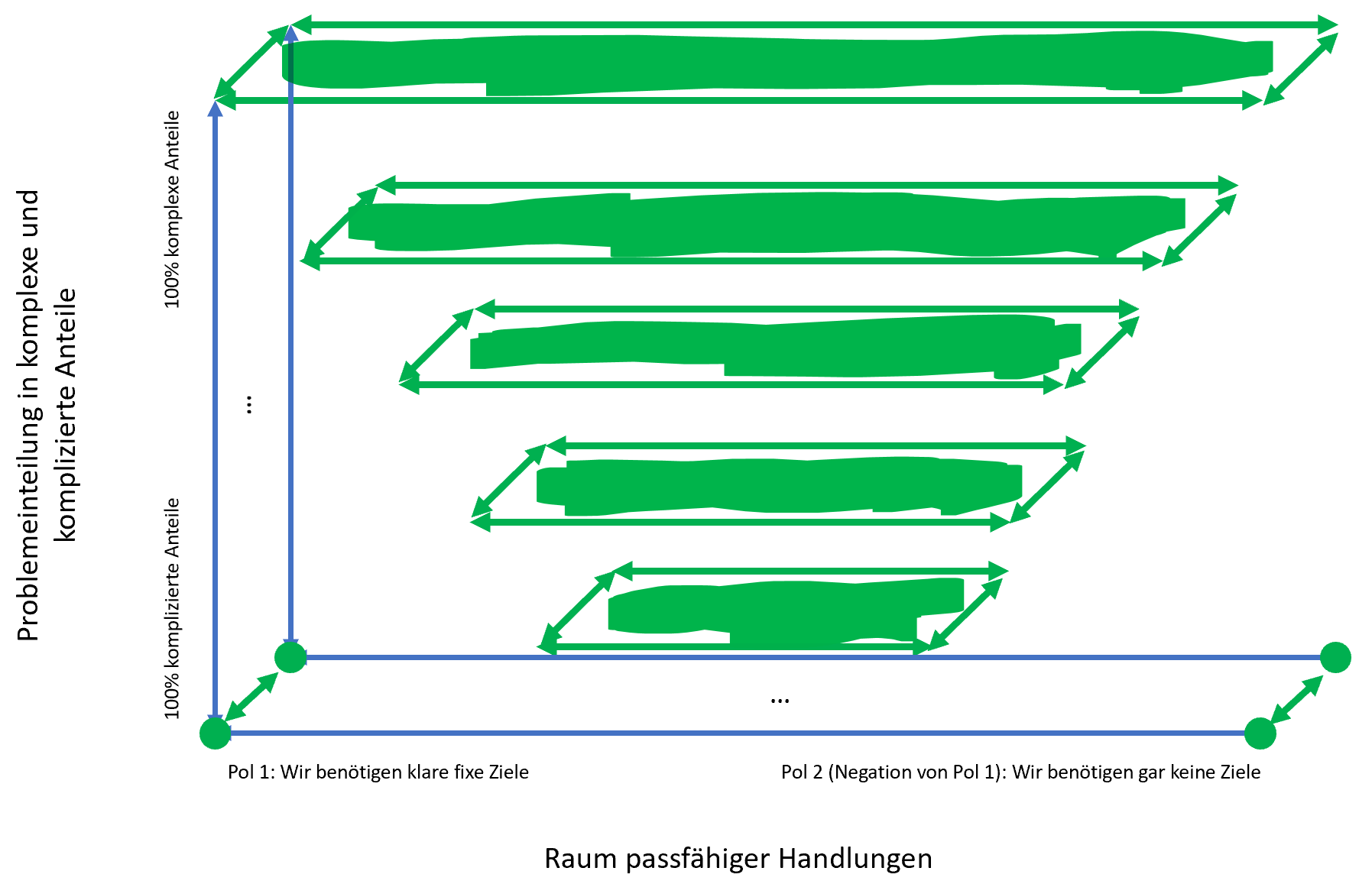
Und nun kommt noch hinzu, dass ich in der obigen Abbildung nur einen Polstrang aufgeführt habe, also nur eine Dimension. Es gibt noch viele mehr, die man beim Lösen von Problemen beachten sollte. Die untere Abbildung stellt das mal schematisch für 2 Polstränge (2 Dimensionen) dar.
Was genau kann man sich unter diesen Polsträngen (Dimensionen) vorstellen? Das sind die Wie-Fragen, die für das Lösen der Probleme relevant sind, also Fragen wie
- Benötige ich ein konkretes Ziel?
- Kann ich eine dedizierte Methode verwenden?
- Sollte ich das Problem im Scrum-Denkrahmen lösen?
- …
Die jeweiligen Extrempole dieser Fragen, also dieser Polstränge, sind dann zum einen eine Antwort auf die Frage, sowie das genaue Gegenteil dieser Antwort. Identifiziere ich also x relevante Frage zum Lösen dieses Problems kommen zu den beiden Achsen der ersten Abbildung genau x Achsen hinzu.
Auffallend ist, dass, je mehr komplexe Anteile ein zu lösendes Problem hat, desto größer ist die Anzahl der zu beantwortenden Wie-Fragen, desto mehr Achsen kommen also hinzu. Das erhaltene Diagramm spannt also einen n-dimensionalen Raum an passfähigen Lösungen auf, in dem die dedizierte Lösung gefunden werden muss.
Und genau für das Auffinden dieser dedizierten Lösung in diesem n-dimensionalen Raum ist die Frage “Wie?” nicht zielführend, ist sie ja bereits im 1-dimensionalen Raum nicht, wie oben ausgeführt. Die Frage “Wer?” ist relevant. Man benötigt also den “richtigen” Menschen mit der passigen Gabe, der sich in komplexen Umgebungen passfähig bewegen kann.


Pingback: Komplexität ist doch auch keine Lösung | Become Viable