Drei Stolperfallen der qualitativen Modellierung

In meinem Post Entscheidungen: Mit System Dynamics dem BI Wirkkreis Leben einhauchen habe ich explizit ausgeführt, wie wichtig System Dynamics für Entscheidungsprozesse ist. System Dynamics ist eine Methode des quantitativen Modellierens. Als Vorstufe des quantitativen Modellierens hat sich aus meiner Erfahrung das qualitative Modellieren bewährt. Um diese Vorteile jedoch nutzbar zu machen, muss man sich über die Stolperfallen von qualitativen Modellen bewusst sein. In diesem Post möchte ich die Möglichkeit nutzen, 3 Stolperfallen zu zeichnen und an eingängigen und einfachen Modellen zu erklären.

Stolperfalle 1: Bestands- und Flussfaktoren

Bei qualitativen Modellen werden in der Regel keine Unterscheidungen nach der Art der Faktoren vorgenommen. Die Verbindungen zwischen den Faktoren, welche die Ursache-Wirkungsbeziehungen darstellen, bekommen in der Darstellung der Modelle ein “+”, wenn die Wirkung des einen auf den anderen Faktors gleichgerichtet ist und ein “-“, wenn diese entgegengesetzt ist. Stellen wir uns vor, wir haben zwei Faktoren. Der erste ist “Motivation der Mitarbeiter” und der zweite “Leistung der Mitarbeiter”. Es ist schnell einleuchtend, dass, wenn die Motivation der Mitarbeiter steigt, die Leistung ebenfalls steigt. Die Verbindung zwischen beiden Faktoren bekommt also ein “+”. Die Wirkung von Motivation auf Leistung ist gleichgerichtet. Würde die Leistung bei steigender Motivation sinken, wäre die Wirkung entgegengesetzt und die Verbindung beider Faktoren müsste mit einem “-” dargestellt werden.

Diese generelle Betrachtungsweise ist aber zu fahrlässig, da sie keine Unterscheidung von Faktoren in Fluss- und Bestand einbaut. Das möchte ich an einem wohl für Jeden bekannten Beispiel, nämlich einer Badewanne darstellen. Stellen Sie sich folgendes Szenario vor. Sie füllen eine Badewanne mit Wasser und drehen dabei den Wasserhahn. Wir betrachten wiederum 2 Faktoren, den Füllstand des Wassers in der Badewanne und die Menge des Wassers, die aus dem Wasserhahn in die Wanne fließt. Bereits an der Beschreibung der beiden Faktoren erkennen wir, dass es sich beim ersten Faktor um einen Bestandsfaktor und beim zweiten um einen Flussfaktor handelt. Kann man zwischen diesen beiden Faktoren eine Ursache-Wirkungsbeziehung darstellen?

1. Der Wasserhahn wird in Richtung “zu” gedreht, aber nicht ganz bis zum Anschlag. Das Wasser, welches aus dem Wasserhahn fließt, wird weniger. Wird dann auch der Wasserstand in der Wanne geringer? Ein ganz klares Nein. Das ist einleuchtend. Auch wenn das Wasser, das aus dem Wasserhahn in die Wanne fließt, geringer wird, wird trotzdem noch Wasser in die Wanne fließen, zwar weniger als vorher, aber immerhin. Der Wasserstand in der Wanne steigt also, und zwar degressiv.
2. Der Wasserhahn wird weiter aufgedreht. Damit wird die Wassermenge, die durch den Wasserhahn in die Wanne fließt, erhöht. Was passiert nun mit dem Wasserstand in der Wanne? Auch klar. Er steigt und diesmal schneller als vorher, also progressiv.
3. Der Wasserhahn wird komplett zugedreht. Es fließt dann kein Wasser durch den Wasserhahn in die Wanne. Damit bleibt auch der Wasserstand in der Wanne stabil, er wird nicht größer und auch nicht kleiner.
4. Der Wasserhahn bleibt unberührt. Dann bleibt die Wassermenge, die durch den Wasserhahn fließt, gleich. Der Wasserstand in der Wanne wird größer, diesmal linear.

An den 4 Fällen erkennen wir, dass wir nach der oben getroffenen Definition nicht eindeutig ein “-” oder “+” zwischen den beiden Faktoren setzen können. Der Wasserstand wird niemals geringer, ganz egal ob der Wasserzufluss kleiner oder größer wird. Nur in einem Fall bleibt der Wasserstand konstant, und zwar im 3., wo der Wasserzufluss gleich Null ist. Damit haben wir die erste Stolperfalle aufgedeckt.

Wir müssen auch in qualitativen Modellen zwischen Bestands- und Flussfaktoren unterscheiden und die Ursache-Wirkungsbeziehungen entsprechend differenzieren.

Auf Grund der Beziehungen zwischen Fluss- und Bestandsfaktoren, wie wir sie im Badewannenbeispiel vorfinden, müssen wir die oben getroffenen Erklärungen für “+” und “-” konkretisieren. Ein Faktor A hat eine gleichgerichtete Wirkung (“+”) auf einen anderen Faktor B, wenn eine Erhöhung (Minderung) des Faktors A, einen Wert für den Faktor B hervorbringt, der größer (kleiner) ist als der Wert von Faktor B, wenn sich der Faktor A nicht geändert hätte. Mit dieser Definition ist die Beziehung zwischen Wasserstand in der Badewanne und Wasserzufluss gleichgerichtet, also “+”.

Stolperfalle 2: Nettoflussraten

Hat man die Unterscheidung nach Bestand und Fluss vollzogen, gilt es eine nächste Stolperfalle zu umschiffen.

Flussfaktoren müssen in Zu- und Abfluss differenziert werden.

In dem oben dargestellten Beispiel mit der Badewanne haben wir explizit keinen Abfluss eingebaut. Wir haben nur einen Zufluss, nämlich den Wasserhahn. Ein Abfluss könnte der Stöpsel in der Badewanne sein, über den das Wasser aus der Wanne abgelassen werden kann. Der Nettofluss wird definiert als Zufluss-Abfluss. Ein Bestand kann also nur abgebaut werden, in diesem Fall das Wasser, wenn der Nettofluss kleiner ist als Null. Das bedeutet, in unserem Beispiel kann das Wasser niemals aus der Badewanne entweichen, da Zufluss-0 niemals kleiner als Null werden kann.

In der Praxis wird dieses Phänomen leicht zur verschleierten Darstellung einer kritischen Situation genutzt. Nehmen wir das Beispiel Umweltverschmutzung durch Ausstoß von Kohlendioxid. Oft höre ich in den Medien, das der Ausstoß von Kohlendioxid gemindert wurde. Was sagt uns das? Nicht sehr viel. Für eine ganzheitliche Bewertung dieses Faktums müssten wir auch noch wissen, wieviel Kohlendioxid abgebaut wurde und wie groß die derzeitige Menge an Kohlendioxid in der Atmosphäre ist. Wir müssen also wissen, wie hoch der Abfluss und der derzeitige Bestand ist. Diese 3 Faktoren müssten wir dann über eine Messreihe über einen längeren Zeitraum betrachten. Ähnlich verhält es sich mit dem Thema Schulden, wo ich auch sehr häufig eine Vermischung von Fluss und Bestand beobachte. Ein Budgetdefizit herrscht beispielsweise im Staatshaushalt vor, wenn die Ausgaben in einem größer sind als die Einnahmen. Das Budgetdefizit ist also eine Nettoflussrate größer als Null, wenn die Schulden der Bestand sind. Wenn also in der Presse geschrieben steht, dass das Budgetdefizit geringer geworden ist, bedeutet es trotzdem, dass der Schuldenberg weiter angewachsen ist. Bei dem Ausweisen von Unternehmensergebnissen ist beispielsweise die Gewinn-und-Verlustdarstellung (GuV) der Fluss, der sich zu der Bilanz als Bestand akkumuliert.

Es ist also extrem wichtig ein Verständnis des Verhältnisses von Fluss und Bestandsfaktoren zu haben, um komplexe und dynamische Sachverhalte richtig interpretieren zu können. Günther Ossimitz hat diesen Fakt als Anlass genommen, Aufgaben diesbezüglich zusammen zu stellen. Diese finden Sie hier. Viel Spaß beim Lösen dieser Aufgaben. Sie können die Lösungen gerne als Kommentar posten. Die Lösungen habe ich natürlich auch vorrätig. Bei Bedarf können Sie diese gerne bei mir anfragen.

Des Weiteren möchte ich auf den Inhalt meines Rucksacks in der Sektion Modellierung verweisen. Dort finden Sie den Screencast 1 mit dem Titel “Beziehungen zwischen Fluß- und Bestandsfaktoren beim quantitativen Modellieren”. In diesem erkläre ich alle möglichen Beziehungen zwischen Fluss- und Bestandsfaktoren. Die Folien, die ich dort erkläre finden Sie hier.

Stolperfalle 3: Versteckte Rückkopplungsschleifen

Ich möchte nun die 3 Stolperfallen abschließend an einem Beispiel demonstrieren. 2 Stolperfallen haben wir bereits besprochen, die Differenzierung der Faktoren in Bestand und Fluss sowie die Nettoflussraten. Diese werden wir in diesem finalen Beispiel noch einmal wiederholen und damit verinnerlichen. Die 3. Stolperfalle, die versteckten Rückkopplungsschleifen, möchte ich Ihnen hier initial nahe bringen.

Das Beispiel nehme ich aus meiner Kinderzeit, wo ich noch sehr häufig mit Cowboys und Indianern in Form von kleinen Hartgummifiguren gespielt habe. Im Rahmen dieser Spiele haben meine Freunde und ich uns auf die Seiten der Indianer respektive der Cowboys aufgeteilt und haben die Hartgummifiguren sich gegenseitig bekriegen lassen. Eines noch vorweg. Selbstverständlich möchte ich mit diesem Beispiel den Krieg oder das Töten nicht verherrlichen.

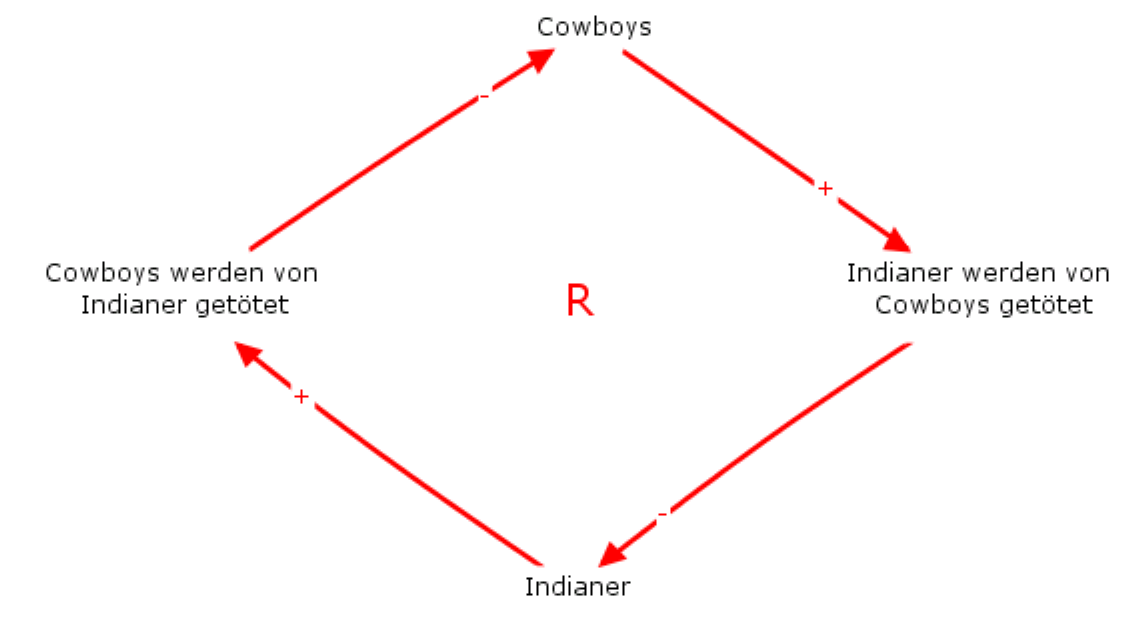
In der folgenden Abbildung habe ich das qualitative Modell ohne Unterscheidung von Bestands- und Flussfaktoren gemalt.

Interpretieren wir diese sich selbst verstärkende Rückkopplungsschleife. Starten wir mit den Indianern und verfolgen den Wirkungskreis im Uhrzeigersinn. Je mehr Indianer im Spiel sind, desto mehr Cowboys werden von Indianern getötet. Das führt dazu, dass es weniger Cowboys gibt, was wiederum dazu führt, dass weniger Indianer von Cowboys getötet werden, was entsprechend dazu führt, dass es mehr Indianer gibt, die dann wieder mehr Cowboys töten. Diesen Kreis kann man jetzt fortsetzen und erkennt sehr schnell, dass die Indianer zahlenmäßig zunehmen und die Cowboys abnehmen. Diese Argumentationskette könnte man auch spiegelbildlich darstellen, dass nämlich die Cowboys in der Anzahl zunehmen und die Indianer entsprechend abnehmen. Das ist das typische Verhalten von sich selbst verstärkenden Rückkopplungsschleifen, das exponentielle Wachstum, wobei das Schrumpfen als negatives Wachstum bezeichnet werden kann.

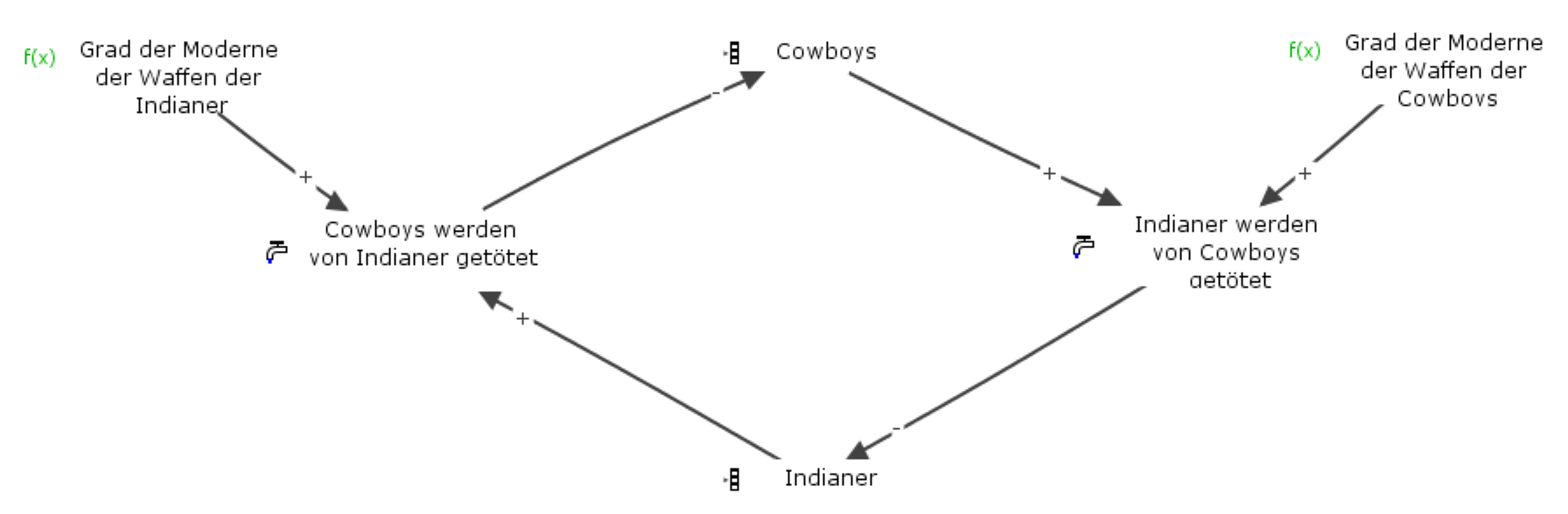
Aber macht das Sinn? Cowboys und Indianer töten sich gegenseitig und eine der beiden Seiten nimmt zahlenmäßig zu? Wir werden also die Stolperfalle 1 aufdecken und das Modell abändern, in dem wir eine Unterscheidung nach der Art der Faktoren machen. Die folgende Abbildung stellt das neue Modell dar.

Wir erkennen jetzt die Faktoren “Indianer” und “Cowboys” als Bestandsfaktoren, die jeweils von einem Flussfaktor geändert werden. Gehen wir nun wieder die Wirkungskette entlang und starten bei dem Bestandsfaktor “Indianer”. Wenn die Anzahl der Indianer steigt, dann steigt auch die Anzahl der Cowboys, die von Indianern getötet werden im Vergleich, als wenn sich die Anzahl der Indianer nicht verändert hätte. Das führt dazu, dass die Anzahl der Cowboys schneller abnimmt, relativ dazu wenn die Anzahl der getöteten Cowboys konstant geblieben wäre. Das bedeutet dann auch, dass die Anzahl der Indianer, die von Cowboys getötet wird, kleiner wird, wiederum relativ dazu das die Anzahl der Cowboys konstant bliebe. Das bedeutet dann, und das ist der Knackpunkt, dass die Indianer zahlenmäßig langsamer schrumpfen. Sie schrumpfen auf jeden Fall, aber eben nicht ganz so rasant. Damit ist also der Knoten gelöst. Sowohl die Indianer als auch die Cowboys schrumpfen zahlenmäßig, nur halt in unterschiedlicher Geschwindigkeit. Und die Geschwindigkeit des Schrumpfens nimmt von Runde zu Runde ab.

Damit haben wir nun auch die zweite Stolperfalle implizit aufgedeckt. An der Argumentationskette erkennen wir, das die Nettoraten beider Flussfaktoren “… werden von …getötet” niemals größer werden als Null. Damit können also auch die Bestände niemals ansteigen. Da wir die Faktoren des Modells nun in Bestands- und Flussfaktoren unterschieden haben, können wir simulieren. Das wollen wir also tun. Sie erkennen in der obigen Abbildung zwei weitere bislang noch nicht erwähnte Faktoren. Das sind so genannte Hilfsfaktoren, in diesem Fall Inputfaktoren, da sie von keinem Faktor des Modells beeinflusst werden. Sie müssen am Anfang der Simulation festgesetzt werden. Diese beiden Faktoren stellen die Modernität der Waffen der Indianer sowie der Cowboys dar. Die Faktoren liegen zwischen 0 und 1. Die Modernität der Waffen ist hoch nahe bei 1 und respektive gering nahe bei 0. Je moderner die Waffen, desto vergleichsweise mehr Gegner können getötet werden. Das folgende Ergebnis erhält man mit folgenden Parametern

1. Grad der Moderne der Waffen der Cowboys = 0.6
2. Grad der Moderne der Waffen der Indianer = 0.3
3. Anfangsbestand der Cowboys = 50
4. Anfangsbestand der Indianer = 80

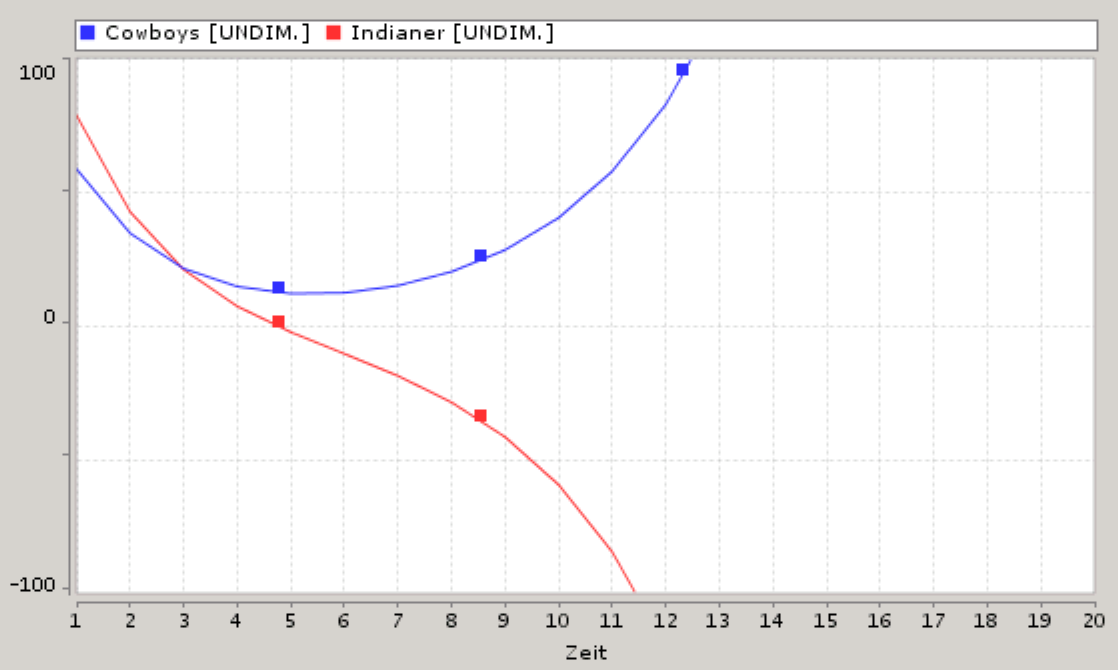
Das Modell finden Sie hier. Wir erkennen, dass die Indianer als auch die Cowboys zahlenmäßig abnehmen, wie eben auch vermutet. Aber ab dem Zeitpunkt 5 beginnen die Cowboys zahlenmäßig anzuwachsen und die Indianer zu schrumpfen, und das exponentiell. Wie ist das zu erklären?

Ab dem Zeitpunkt 5 wird die Anzahl der Indianer negativ. Das kann ja nicht sein. Im Modell sind also essentielle Beziehungen noch nicht abgebildet, und zwar die, dass die Bestände der Indianer und Cowboys nicht negativ werden darf. Es existieren also versteckte Rückkopplungsschleifen. Stolperfalle 3 ist aufgedeckt.

Versteckte Rückkopplungsschleifen müssen sichtbar gemacht werden.

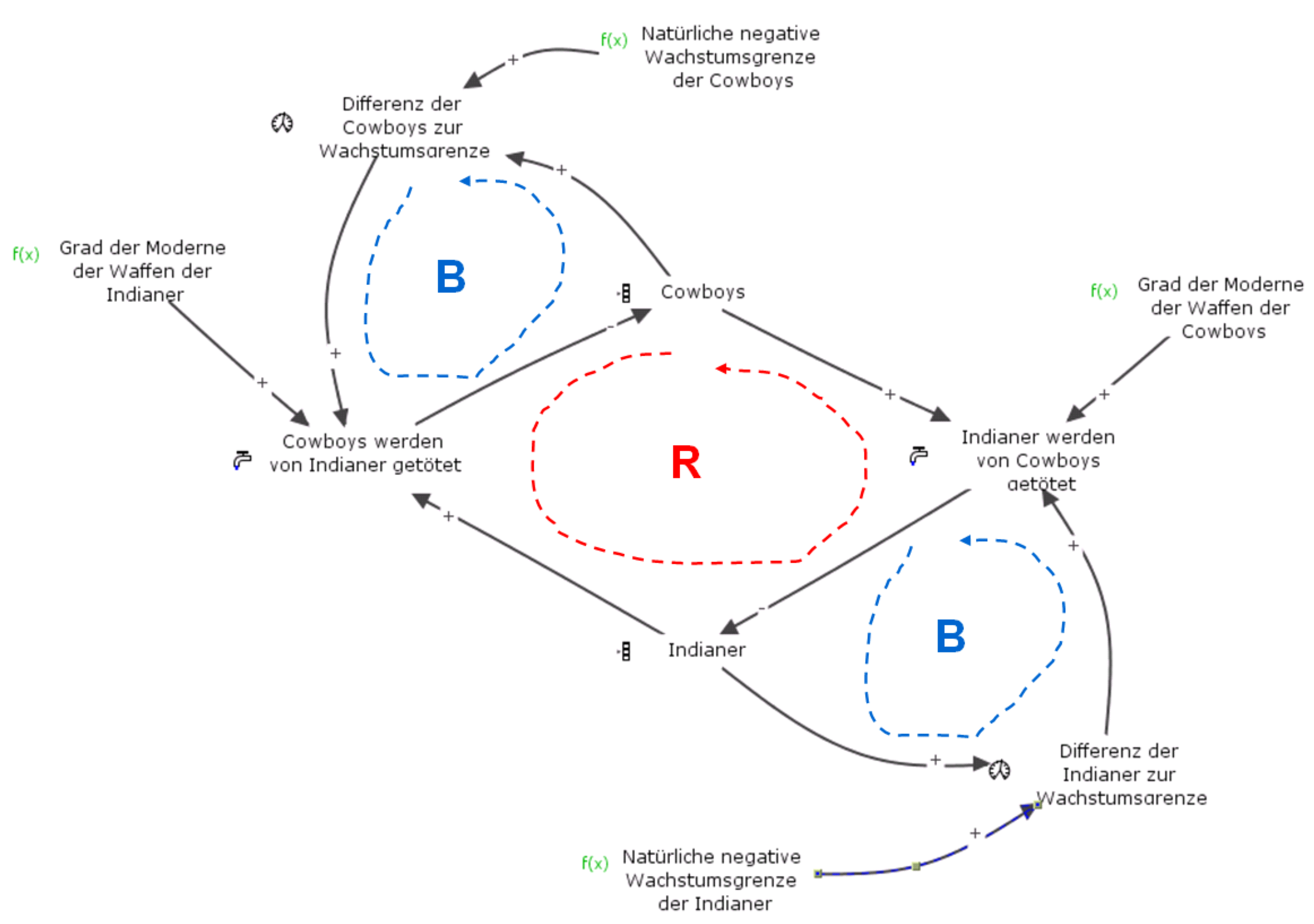
Die folgende Abbildung zeigt die beiden versteckten Rückkopplungsschleifen, die die Anzahl der Cowboys und der Indianer nach unten hin beschränken, und deshalb sich ausgleichende Rückkopplungsschleifen sind. Das ist mit einem “B” gekennzeichnet.

Dieses Modell ergibt das folgende Ergebnis, wenn man für die Simulation die obigen Parameter zu Grunde legt.

Fazit

Wenn man jetzt die initial getätigte Aussage, dass nämlich die Cowboys bzw. die Indianer exponentiell wachsen bzw. schrumpfen mit der obigen Abbildung vergleicht, erkennen wir wie fatal die Analyse von Problemsituationen sein kann, wenn die 3 in diesem Post aufgezeigten Stolperfallen der qualitativen Modellierung nicht aufgedeckt werden.

(Keine Bewertungen bislang. Geben Sie doch die erste ab.)

Loading...