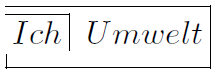Die 3 Elemente von Kommunikation, MEINEN, MITTEILEN und VERSTEHEN, sowie die sich auf ihre Basis aufbauenden GrundFORMen von Kommunikation und Kombination dieser, habe ich in den letzten beiden Beiträgen Kommunikation: Du komisches geheimnisvolles ETWAS und Die 6 GrundFORMen der Kommunikation angereicht.
Im 2. Beitrag habe ich SelFis erwähnt und dabei auch auf den Beitrag von Gitta Peyn verwiesen, in dem sie SelFis zur Analyse von Kommunikationsmuster verwendet hat. SelFis werden berechnet. Und um genau dieses Rechnen geht es mir in diesem Beitrag, dem letzten und dritten meiner Trilogie zu Kommunikation. Ich werde erklären, wie sich diese SelFis, mit denen ich Muster von Kommunikation aufdecken kann, errechnen.
Dazu passend ein Zitat von Heinz von Förster, welches ich diesem Interview entnommen habe.
Das Nervensystem lässt sich, ausgehend von diesen Annahmen, als eine Art Rechner interpretieren, der ein logisches Kalkül durchführt. Und ein Neuron erscheint aus dieser Perspektive als ein Operator, der solche logischen Funktionen berechnet.
Ich kann also im Kontext von Kognition und Kommunikation getrost von Rechnen sprechen.
Wie beobachten und begreifen wir Welt?
Wir Menschen erkunden Welt über genau eine Operation: indem wir unterscheiden. Wir fokussieren auf etwas in Welt, Inhalt, und setzen dass dann in einen Kontext. Es macht einen Unterschied, ob ich ein bestimmtes Gemälde (Inhalt) in einer Gemäldegalerie (Kontext) oder bei mir zu Hause (Kontext) beobachte und fokussiere.
Das möchte ich an einem einfachen Beispiel spiegeln. Ich möchte Obst kaufen. In meiner Stadt Rostock gibt es verschiedene Möglichkeiten Obst zu kaufen.
- Schritt: Ich entscheide mich für den Ostseepark. Alle anderen möglichen Einkaufsparks und Geschäfte werden Kontext.
- Schritt: Im Ostseepark entscheide ich mich für “Real”. Alle anderen Geschäfte im Ostseepark werden Kontext.
- Schritt: Im “Real” entscheide ich mich für den Obststand. Alle anderen Stände im “Real” werden Kontext.
- Schritt: Am Obststand angekommen entscheide ich mich für das Apfelregal. Alle anderen Obstregale werden Kontext.
- Schritt: Vor dem Apfelregal entscheide ich mich für die roten Äpfel. Alle anderen Äpfel werden Kontext.
Diese von mir getätigten Operationen kann man nun mathematisch so ausdrücken.
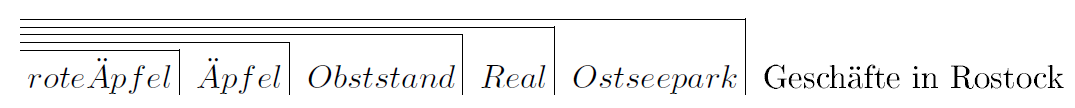Aus den ersten beiden Beiträgen dieser Triologie zur Kommunikation erkennen Sie sicher die Haken wieder.
Für jede mathematische Operation benötige ich natürlich auch Werte. Für die Operation des Unterscheidens möchte ich nun 4 Werte an dem oben eingeführten Beispiel des Obstkaufens erklären.
- Wert: Markiert
Im Schritt 5 habe ich mich vor dem Apfelregal stehend für die roten Äpfel entschieden. Ich markiere die roten Äpfel.
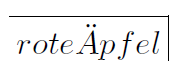
- Wert: Nicht markiert
Im Schritt 5 habe ich mich vor dem Apfelregal stehend für die roten, nicht für die grünen Äpfel entschieden. Die grünen Äpfel markiere ich nicht, sie sind Kontext.
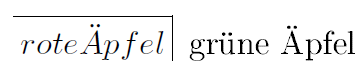
- Wert: Unbestimmt
Ich weiß heute noch nicht, ob ich morgen, wenn ich vor dem Apfelregal stehe, für die roten oder für die grünen Äpfel entscheiden werde. Hier ist der so genannte Re-Entry zu sehen, den wir auch schon im zweiten Beitrag im Rahmen der 6 GrundFORMen von Kommunikation gesehen haben. Dazu komme ich gleich noch einmal zu sprechen.
- Wert: Imaginär
Ich stelle mir vor, dass ich mich morgen, wenn ich vor dem Apfelregal stehe, für die roten Äpfel und nicht für die grünen Äpfel entscheiden werde.
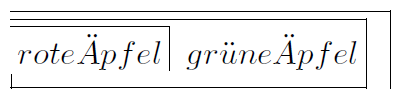
Was bedeutet nun Re-Entry? Dass die FORM immer wieder in sich selbst eingefügt wird. So lässt sich beispielsweise Selbstbeobachtung abbilden: Wir betrachten uns selbst. Derjenige, der sich selbst beobachtet, ist Ich, das, was er beobachtet, Umwelt.
Dann gehen wir zu Selbstbezüglichkeit weiter, indem uns bewusst wird, dass wir in unserer Selbstreflexion immer wieder eine Paradoxie ausdifferenzieren, nämlich die von Identität: Wer ist derjenige, der beobachtet und was ist das, was beobachtet wird? Wann wird das, was beobachtet wurde, zu demjenigen, der beobachtet? ad infinitum …
Ich betrachte mich selbst. In diesem Prozess bin ich mal markiert und mal nicht markiert, immer im Wechselspiel. In dem Moment, wo ich mich fokussiere, wird das, was ich fokussiere, Umwelt und nicht mehr ich, denn ich beobachte ich mich ja selbst. Allerdings beobachtet ja auch jemand, nämlich “Ich”.
Damit wird Unbestimmtheit modelliert, die bei Lebendigkeit niemals aufgelöst wird, sonst stirbt Lebendigkeit. Lebendigkeit konstituiert sich an Unbestimmtheit.
Allerdings, und nun komme ich zu dem Apfelbeispiel zurück. Menschen, die Unentscheidbarkeit in Alltagssituationen nicht auflösen können, können darunter leiden. Wer die Wahl nicht mehr zu treffen vermag, erstarrt in inneren Konflikten. Stellen Sie sich vor, ich stehe vor dem Apfelregal und entscheide mich stetig hin und her: Rote Äpfel -> Grüne Äpfel -> Rote Äpfel -> Grüne Äpfel -> … Meine Frau würde mich vielleicht nie wieder bei uns zu Hause zu Gesicht bekommen, da ich den Einkaufsvorgang nicht beenden kann.
In dem Moment, in dem ich mich entscheide, damit den Entscheidungsprozess beende und die FORM bestimme, beende ich Unbestimmtheit. Ich kann aber auch komplexe Entscheidungen damit beenden, dass ich feststelle: Die FORM ist unbestimmt, wie bei Identität.
Bislang hatten wir Operationen und Werte. Um rechnen zu können benötigen wir noch Axiome, also Vorschriften oder Regeln, wie wir rechnen sollen. 2 dieser Axiome, die sich ausschließlich auf die Werte “markiert” und “nicht markiert” beziehen, erkläre ich nun.
- Rechenregel: Kondensation
Wenn ich etwas erneut unterscheide, dann ist der Wert der gleiche wie bei einer einmaligen Unterscheidung. Wenn ich mich für rote Äpfel entscheide und diese Entscheidung wiederhole, dann ändert sich das Ergebnis nicht. Egal, wie häufig ich “rote Äpfel” denke, es bleiben rote Äpfel.
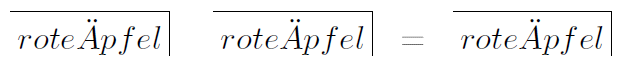
- Rechenregel: Aufhebung
Wenn ich eine Unterscheidung abermalig fokussiere, dann ist das Unterschiedene verschwunden. Wenn ich mich für rote Äpfel entscheide und über diese Entscheidung nachdenke, diese also fokussiere, dann sind die roten Äpfel aus meiner Fokussierung verschwunden. Die linke Seite der folgenden Gleichung und “gar nichts” sind äquivalent: Leere.
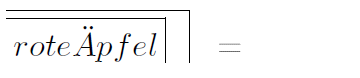
Für das komplette Axiomensystem, in dem auch Regeln für das Rechnen mit den Werten “unbestimmt” und “imaginär” enthalten sind, verweise ich gerne auf unseren Ausbildungsgang zum Komplexitätsorganisator, wo wir dieses Axiomensystem ausführlich herleiten werden. Wer darauf nicht warten möchte, kann sich auch gerne per Selbststudium mit dem Buch uFORM iFORM von Ralf Peyn und dort konkret im Abschnitt “Rechnen mit Unbestimmten und Imaginären” helfen. Darauf hier noch tiefer einzugehen, würde inhaltlich erst einmal überfordern.
So, nun haben wir Alles beisammen. Wir haben Operation, Werte und Rechenregeln. Nun können wir uns anschauen, wie die so genannten SelFis, auf die Gitta Peyn in ihrem Beitrag Konfliktdynamiken mit SelFis untersuchen eingeht, errechnet werden.
Wie errechnen sich SelFis?
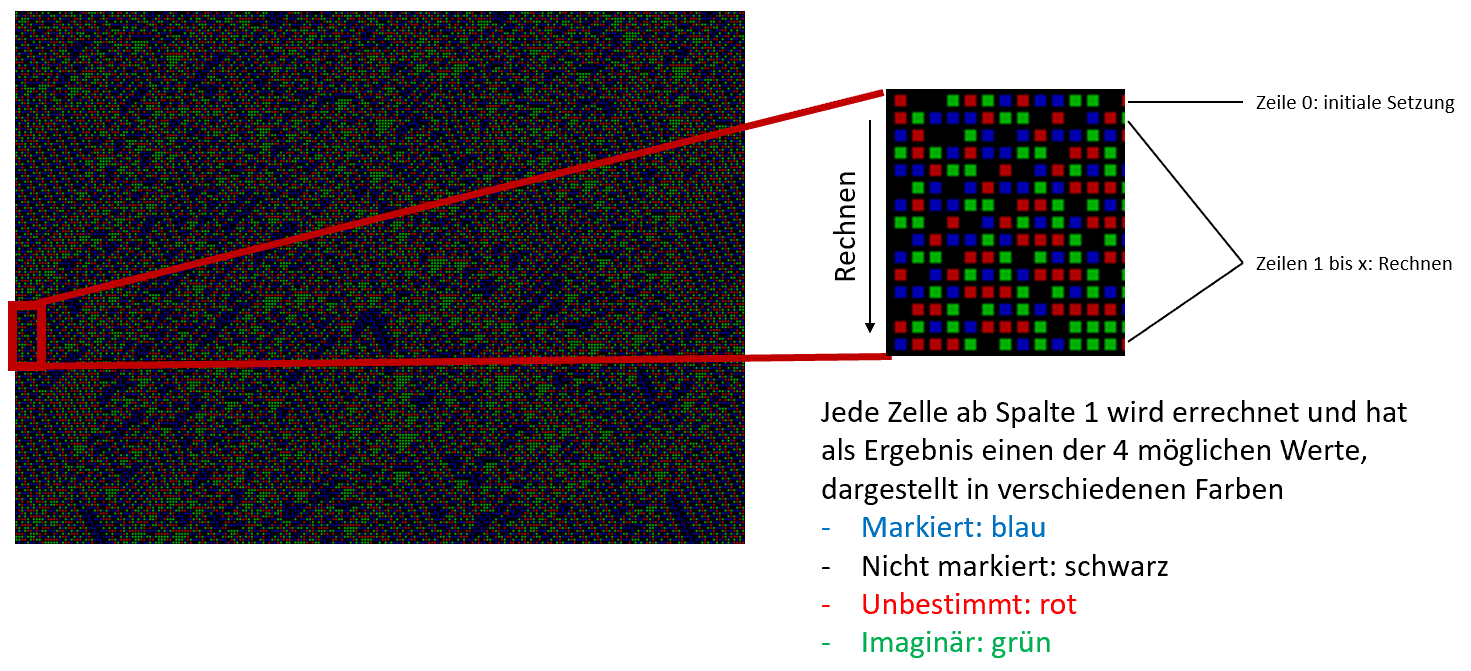
Zur Erklärung der Berechnung nehme ich das SelFi “TalkToMe (Komplexes Driften)”, das ich am Ende des zweiten Beitrages dieser Trilogie bereits angerissen habe. In der folgenden Abbildung sehen wir auf der linken Seite das SelFi und auf der rechten einen vergrößerten Ausschnitt.
Wie in der obigen Abbildung dargestellt, wird die nullte Zeile initial gesetzt. Das könnte ich vergleichen mit dem Vorgeben eines bestimmten zu diskutierenden Themas für 2 Menschen, innerhalb eines Teams, eines Unternehmens etc. Die weiteren Zellen in den Zeilen 1 bis x werden zellenweise von links nach rechts und von oben nach unten errechnet. Dabei errechnen sich die Zellen in den Zeilen n+1 ausschließlich aus den Zellen der Zeile n.
Das Kommunikationsmuster “TalkToMe (Komplexes Driften)” setzt sich aus den folgenden beiden GrundFORMen von Kommunikation zusammen. Das habe ich im letzten Beitrag dieser Trilogie bereits ausgeführt.
Bevor wir rechnen können, nehmen wir noch eine Setzung vor.
- Meinen = L
- Mitteilen = E
- Verstehen = R
Damit ergibt sich folgende KommunikationsFORM.
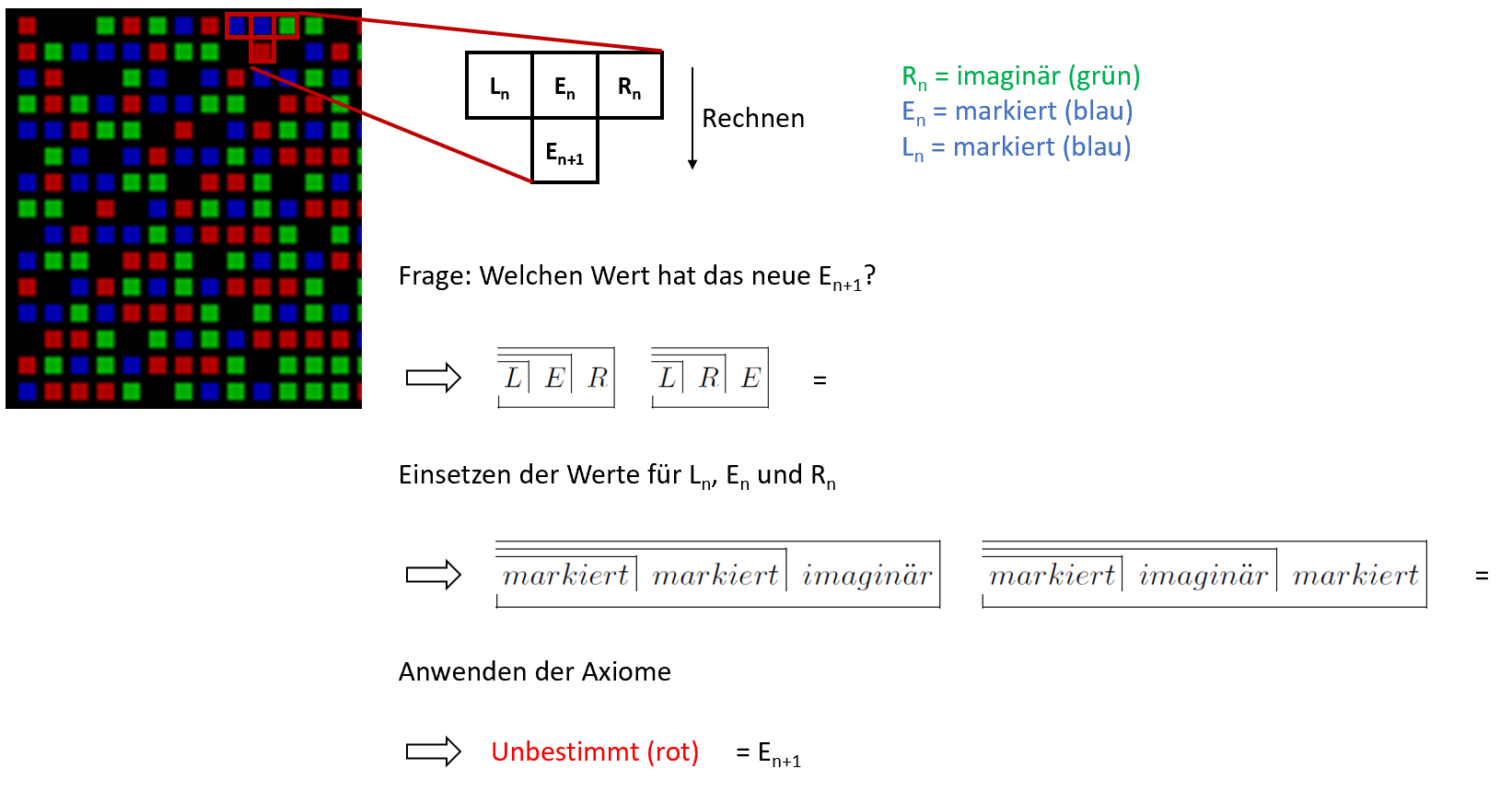
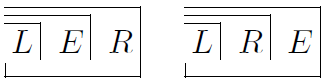Warum können wir diese Setzung vornehmen? Ein Gedanke En+1 der Zeiteinheit n+1 FORMt sich weiter und zwar aus denen der nahen Vergangenheit n (En) und den Nachbargedanken, links (Ln) und rechts (Rn). Jede Zelle „E“ der Zeile n+1 errechnet sich aus den 3 Nachbarzellen “L”, “E” und “R” der Zeile n. Die folgende Abbildung stellt das Rechenbeispiel für eine dedizierte Zelle exemplarisch dar.
Jede Zelle wird nun getreu dieser beschriebenen Vorgehensweise zeilenweise von oben nach unten berechnet. Diese Berechnungsvorschrift ist von Zellulären Automaten bekannt.
Natürlich müssen die SelFis, um Kommunikationsdynamiken mittels dieser zu untersuchen, nicht immer manuell berechnet werden. Das wäre viel zu zeit- und energieaufwändig. Peter Hofmann hat zum automatischen Berechnen der SelFis eine schöne Applikation programmiert, auf die ich gerne verweise. Die obigen Graphiken habe ich übrigens mit diesem Tool erstellt.
Mit diesem Beitrag war mir wichtig zu zeigen, dass sich die SelFis nicht beliebig berechnen, sondern nach einer konkreten Vorschrift, die sich auf das menschliche Rechnen im Rahmen von Kognition bezieht.
(2 Bewertung(en), Durchschnitt: 5.00 von 5)
Loading...