Mit System Dynamics Dynamiken und Verzögerungen von Handlungen verstehen

Kürzlich nächtigte ich im Rahmen einer Geschäftsreise in einem Hotel. Ich habe morgens geduscht. Das Wasser war kalt. Ich drehte den Wasserhahn in Richtung warm. Es tat sich nichts. Ich drehte weiter und auf einmal wurde das Wasser zu heiss. Ich drehte also wieder zurück in Richtung kalt. Dieses Hin- und Herdrehen des Wasserhahnes vollzog ich einige Male bis ich die richtige Wassertemperatur eingestellt hatte. Kennen Sie dieses Phänomen auch?

Warum war ich nicht auf Anhieb in der Lage, anhand des Drehen des Wasserhahns, die richtige Temperatur des Wassers einzustellen? Es lag daran, dass zwischen der Zeit des Drehens des Wasserhahns und des Spürbarwerdens der Wassertemperatur, sprich zwischen Aktion und Ergebnis der Aktion, eine Verzögerung stattfand, die ich nicht gleich einschätzen konnte. Und genau um dieses Thema möchte ich in diesem Post meine Gedanken kreisen lassen: Verzögerungen von Handlungen.

Eines vorweg. Ich werde in diesem Post insbesondere auf System Dynamics, als eine Art der quantitativen Modellierung, und auf einige praktische Beispiele eingehen. Aus meiner Sicht schafft dies eine Basis, Verzögerungen besser zu verstehen. Die Modelle, auf die ich in diesem Post eingehe und die sie auch herunterladen können, sind mit dem CONSIDEO MODELER erstellt.

Für eine ausführliche Einführung in System Dynamics verweise ich gerne auf dieses umfassende Dokument. Es ist allerdings in englischer Sprache verfasst. Ich habe nichts vergleichbar Umfassendes in deutscher Sprache gefunden. Falls Sie fündig geworden sind, können Sie Ihre Rechercheergebnisse gerne posten. Danke.

Was kann man sich unter Verzögerungen vorstellen?

Verzögerungen lassen sich unterscheiden nach der Ordnung und nach dem Typ. Beginnen wir mit dem Typ von Verzögerungen.

Verzögerungen nach Typ

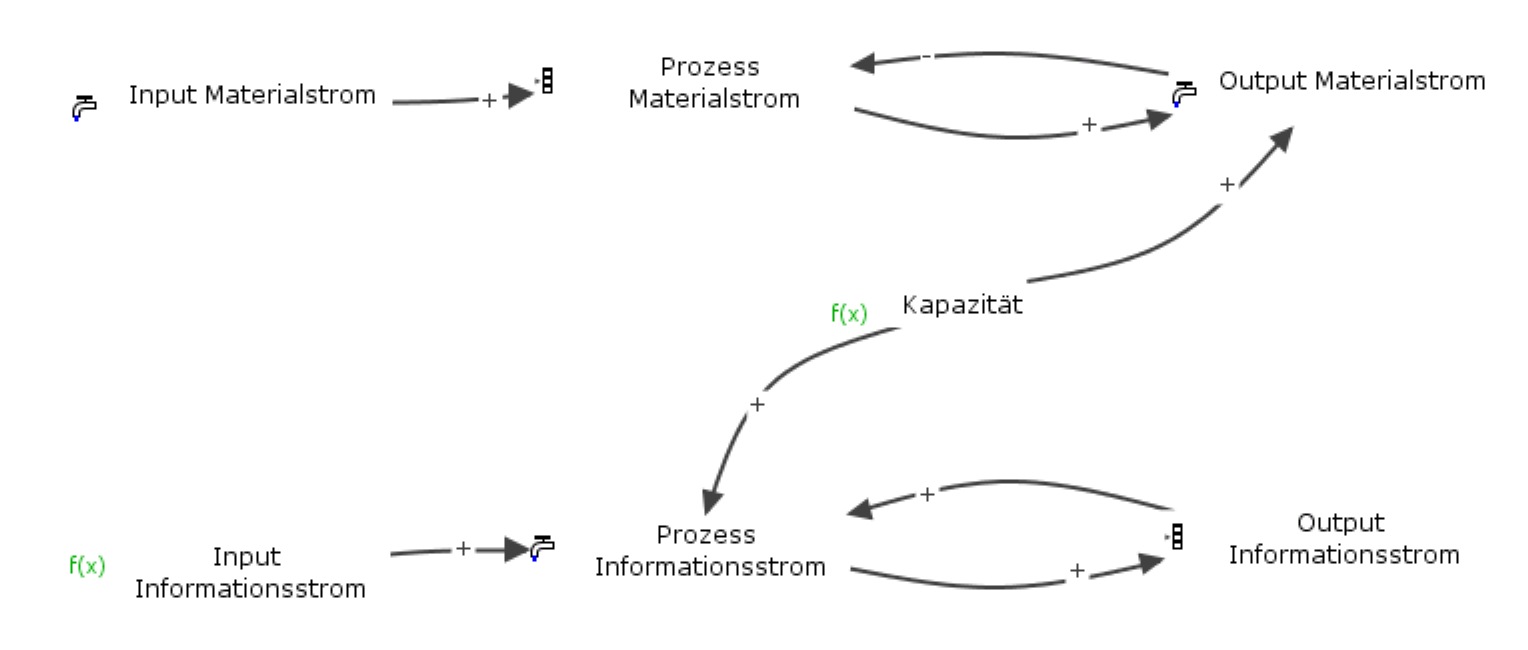
Zwei Typen von Verzögerungen existieren, Verzögerungen in Material- und Informationsströmen. Beide Ströme hängen unmittelbar zusammen. Das eine gibt es nicht ohne das andere. Information kann nur durch Materie übertragen werden und jede Materie enthält auf eine bestimmte Art und Weise Daten, die zu Information verarbeitet werden. Das möchte ich am Beispiel einer Heizungsanlage erklären. Eine Heizungsanlage transportiert Wasser in die Heizungskörper der zu versorgenden Räume, um dort die Temperatur zu regulieren. Der Wasserstrom in der Heizungsanlage ist der Materialstrom und der Transport der Temperatur durch den Wasserstrom ist der Informationsstrom. Man erkennt relativ einfach den oben angesprochenen Zusammenhang, das eines oder das andere nicht existieren kann. Was ebenfalls offensichtlich ist, sind die Verzögerungen. In dem man die Heizung am Thermostat regelt, wird nicht von jetzt auf gleich das Wasser in allen Heizungskörpern der Räume vorhanden sein und mit dem Wasser natürlich auch nicht die Wärme des Wassers, welche die Temperatur im Raum beeinflusst. So lange die am Thermostat eingestellte Solltemperatur noch nicht erreicht ist, verhalten sich beide Verzögerungen identisch. Sie streben asymptotisch ihrem Gleichgewicht entgegen. Erst im Gleichgewicht wird der Unterschied sichtbar.

Erkennen können Sie dieses Phänomen in dem Submodell “nach Typ” des folgenden Modells. Ich habe in diesem Modell absichtlich andere praktische Beispiele modelliert, um den Unterschied zwischen Material- und Informationsverzögerungen an unterschiedlichen praktischen Konstellationen sichtbar werden zu lassen. Für die Materialverzögerung habe ich die Fehlerabarbeitung in IT-Projekten, für die Informationsverzögerung das Erlernen von Schulstoff modelliert. Sie können 3 Parameter einstellen.

• sprung1: initialer Input für die Ströme. Die Dauer der Fehlerbehandlung, also die Zeit die benötigt wird um einen Fehler abzuarbeiten, für den Materialfluss und die Lernzeit, die benötigt wird, um den zu lernenden Stoff zu erlernen.
• sprung2: Input, auf den der initiale Input (sprung1) erhöht oder verringert wird
• step: Der Zeitschritt, bei dem der Input sprung2 erhöht oder verringert wird

Voreingestellt im Modell sind sprung1 = 5, sprung2 = 10 und step = 250. Das erkennen Sie im Simulationscockpit “nach Typ”. Bis zum Zeitschritt 250 verhalten sich beide Ströme, Material- und Informationsstrom identisch. Die Kurven überlagern sich. Ab dem Zeitschritt 250 ist der Unterschied sichtbar. Zu diesem Zeitpunkt befinden sich beide Flüsse schon lange im Gleichgewichtszustand. Die Outputs (Fehler behoben bei Materialstrom und gelernter Stoff bei Informationsstrom) bleiben konstant und sind gleich dem Input. Im Zeitschritt 250 wird der Input von 5 auf 10 erhöht. Im Materialstrom ist das gleichbedeutend mit einer höheren Zeit, die für die Abarbeitung pro Fehler benötigt wird. Im Informationsstrom wird die Lernzeit erhöht. Beim Informationsstrom ändert sich der Output danach nicht, wenn die Lernzeit verkürzt oder verlängert wird. Es wurde ja bereits Alles gelernt. Es kommt keine Information dazu. Es wird zwar noch etwas vermittelt, aber eben nichts Neues mehr, da das Gleichgewicht ja erreicht ist. Deshalb wird auch keine Information mehr erzeugt, sondern nur noch Daten transferiert. In den Diagrammen erkennt man es daran, das der Output stabil bleibt und das der Prozessfluss gleich 0 ist. Beim Materialstrom ist das anders. Es wird der Gleichgewichtszustand verlassen und danach konvergiert Fluss und Prozess wieder gegen den Gleichgewichtszustand, der sich allerdings im Prozess geändert hat. Auch das ist aus einer Erklärungsperspektive einleuchtend. Wenn mehr Zeit benötigt wird, um Fehler abzuarbeiten, muss sich die Anzahl der behobenen Fehler pro Zeiteinheit erst einmal verringern. Diese Anzahl, sprich der Output, pendelt sich aber nach einer gewissen Zeit wieder auf die gleiche Anzahl ein, jedoch auf Kosten der im Prozess befindlichen Fehler. Die Anzahl der Fehler in Bearbeitung pendelt sich nämlich auf ein höheres Gleichgewicht ein.

Bitte beachten Sie, dass diese Untersuchungen bei konstantem Input vorgenommen wurden, nur die Kapazitäten wurden geändert. Sie können im Modell auch gerne andere Konstellationen, beispielsweise konstante Kapazitäten und variable Inputs, testen und das Verhalten verifizieren. In der Struktur beider Ströme erkennen Sie auch den generellen Unterschied, der zu diesem unterschiedlichen Verhalten im Gleichgewicht führt. Im Materialstrom ist der Output ein Flussfaktor und der Prozess ein Bestandsfaktor, beim Informationsstrom ist das umgekehrt der Fall.

Verzögerungen nach Ordnung

Material- als auch Informationsverzögerungen, wie wir sie oben beschrieben haben, lassen sich noch einmal jeweils nach der Ordnung unterscheiden. Ich möchte mich hier auf die Materialverzögerungen beschränken und die Unterscheidung nach der Ordnung vornehmen. Die Erkenntnisse lassen sich auf Informationsverzögerungen übertragen. Materialverzögerungen n-ter Ordnung haben n Makroelemente in der Kette des Materialstromes, die für die Verzögerung verantwortlich sind. Diese Makroelemente werden bei der System Dynamics Modellierung in Form von Bestandsfaktoren dargestellt. In dem Submodell “nach Ordnung” des folgenden Modells habe ich die Fehlerabarbeitung in einem Projekt modelliert. Das Modell, das eine Verzögerung 1. Ordnung darstellt, besitzt ausschließlich einen Bestandsfaktor: Fehler in Bearbeitung. Das Modell, das eine Verzögerung 3.Ordnung abbildet, ist bzgl. der Fehlerabarbeitung in 3 Phasen aufgeteilt, was letztlich zu 3 Bestandsfaktoren führt: Fehler in Analyse, Fehler in Implementierung und Fehler im Test. Beide Modelle zeigen ähnliches Verhalten. Unterschiede zeigen sich in der initialen Reaktion auf den Input. Bei der Verzögerungen 3. Ordnung reagiert das System später als bei der Verzögerung 1. Ordnung, erreicht aber dafür früher das Gleichgewicht, in welchem Input gleich Output ist. Das erkennen Sie im Simulationscockpit “nach Verzögerung” im Diagramm Output, in dem Sie die Kurven “1_Fehler behoben” und “3_Fehler behoben” vergleichen. Die Kapazitäten bei beiden Verzögerungsordnungen sind 20 Zeiteinheiten. Das erkennen Sie an den Parametern “Kapazität 1. Ordnung” und “Kapazität 3. Ordnung”. Daran erkennen wir also, dass sich ein Materialstrom eher in sein Gleichgewicht schwingt, wenn mehrere Makroelemente für die Verzögerungen beteiligt sind.

Des Weiteren erkennen wir sehr schön den jeweiligen Bestand an Bearbeitung von Fehlern im Gleichgewichtszustand, wenn also Input gleich Output ist. Der ergibt sich aus der einfachen Formel Input * Kapzität. In dem Modell 1. Ordnung werden 20 Fehler je Zeiteinheit gefunden und es werden 20 Zeiteinheiten benötigt, um einen Fehler zu bearbeiten. Das ergibt also 400 Fehler. Das sehen Sie im Cockpit “nach Verzögerung” im Diagramm “Prozess” an der Kurve “1_Fehler in Bearbeitung”. Das Gleichgewicht ist übrigens dann erreicht, wenn je Zeiteinheit 20 Fehler behoben werden (Diagramm “Output”). Im Modell ergibt sich der Bestand an bearbeiteten Fehlern additiv aus den 3 Phasen Analyse, Implementierung und Test. Aber auch im Gleichgewichtszustand haben wir in Summe 400 Fehler in Bearbeitung: 60 in der Analyse (20 Fehler * 3 Zeiteinheiten), 200 in der Implementierung (20 Fehler * 10 Zeiteinheiten) und 140 im Test (20 Fehler * 7 Zeiteinheiten).

Wann Sie welche Ordnung der Verzögerung modellieren, hängt häufig vom Detaillevel des Modells ab. Denn im Detail zeigen die verschiedenen Ordnungen unterschiedliche Muster, was wir eben gesehen haben. Verzögerungen nach Ordnung sind genau dann sehr gut zu analysieren, wenn die Bestandsfaktoren, die für die Verzögerungen verantwortlich sind, sichtbar sind. Schwierig wird es, wenn das nicht der Fall ist. Nehmen Sie das Beispiel Alkoholkonsum. Ein Mensch trinkt Alkohol, die Wirkung des Alkohols stellt sich jedoch mit Zeitverzug ein. Wie groß dieser Zeitverzug ist, ist nicht offensichtlich, was viele Menschen dazu verleitet einen “über den Durst” zu trinken. Ein anderer Fall ist der Gartenschlauch, den Sie offen auf dem Rasen ausliegen haben. Drehen Sie den Wasserhahn auf, können Sie relativ gut abschätzen, wann Sie das Wasser am Ende des Schlauchs erwarten können. Nehmen Sie mein Eingangsbeispiel mit der Dusche im Hotel. Da war das nicht der Fall. In der Praxis trifft man häufiger auf Fälle, wo die Verzögerungselemente nicht sichtbar sind.

Ein konkretes Beispiel

Ich möchte die eben gewonnenen Erkenntnisse nutzen, um an einem ganz konkreten Beispiel, nämlich dem Bugfixing, gewisse Sachverhalte zu reflektieren, die ohne ein System Dynamics Verständnis nicht zu Tage gefördert werden können. Das Modell finden Sie hier.

In einer ersten Untersuchung wollen wir schauen, welche Auswirkungen, dass Verteilen von Aktivitäten auf mehrere Instanzen im Rahmen das Bugfixings hat, natürlich unter der Annahme, das die Bearbeitungszeiten für einen Fehler im Durchschnitt identisch sind. Im Modell der 1. Ordnung beträgt diese 9 Zeiteinheiten, im Modell der 3. Ordnung sind es in Summe auch 9 Tage: 2 für Analyse, 4 für Implementierung und 3 für Test. Diese Einstellungen können Sie auch ändern. Das tun Sie im Simulationscockpit “Vergleich der Ordnungen” in den beiden oberen Parameterfenstern. Achten Sie aber bitte immer darauf, dass die Bearbeitungszeiten identisch sind. Wir sehen, dass im Falle der Aufsplittung der Aktivitäten (3. Ordnung), die ersten Fehler später zurück in die Produktion gehen, als wenn man die Aktivitäten nicht aufsplittet (1. Ordnung). Allerdings erreicht man mit der Aufsplittung der Aktivitäten schneller einen effektiven Fluss der Fehler durch die Bearbeitungskette. Das Gleichgewicht wird also früher erreicht. Das führt dazu, dass die Fehler auch früher final abgearbeitet sind: Im Falle, dass ab dem 150. Zeitschritt keine Fehler mehr generiert werden (Simulationscockpit “Parameter”: Variable step) ist das ab der 175. Zeiteinheit der Fall. Im anderen Fall hat man erst ab der 193 Zeiteinheit keine Fehler mehr in Bearbeitung. Diese Erkenntnis gewinnen Sie nach dem Simulieren im Cockpit “Vergleich der Ordnungen”. Haben Sie gewusst, dass eine Aufsplittung der Aufgaben dieses Mehr an Effizienz schafft? Was wir natürlich in diesem Modell vernachlässigt haben, ist, dass die Kommunikation und Übergabe zwischen den Phasen der Fehlerabarbeitung ohne Zeitverzug abläuft. Wir nehmen also an, dass die Effektivität der Fehlerabarbeitung für die beiden betrachteten Fälle konstant ist.

Konzentrieren wir uns nun einzig und allein auf das Modell 3. Ordnung, also auf die Aufsplittung der Aktivitäten, erhalten wir auch einige erstaunliche Einsichten in die Dynamik (Simulationscockpit “3. Ordnung”). Für die Analyse behalten wir die oben vorgenommenen Einstellungen der Kapazitätsvariablen bei: 2 für Analyse, 4 für Implementierung und 3 für Test. Es ist erstaunlich, wie lange benötigt wird, um das Gleichgewicht zu erreichen, sprich bis man genauso viele Fehler pro Zeiteinheit behoben hat, wie sie pro Zeiteinheit generiert werden. Es sind ca. 46 Zeiteinheiten. Des Weiteren erstaunt es, wie lange benötigt wird, um die Fehlerpipeline zu leeren, wenn bereits keine Fehler mehr pro Zeiteinheit generiert werden. Wenn ab der 150. Zeiteinheit keine Fehler mehr erzeugt werden, ist erst ab der 195. Zeiteinheit kein Fehler mehr zu bearbeiten.

Man kann bereits an dieser einfachen Kette die Phänomene der Theory of Constraints (ToC) simulieren und testen. Details zu ToC finden Sie in meinem Rucksack unter Critical Chain Project Management (CCPM). Sie können beispielsweise, in dem Sie die Kapazitätsvariablen für Analyse, Implementierung und Test ändern, erkennen, dass der Durchsatz der Fehler durch die gesamte Kette stark vom schwächsten Glied, vom Engpass, abhängt. Der Engpass ist diejenige Phase, die am längsten dauert. Der Engpass bestimmt also, wann die Fehler final abgearbeitet sind.

Eine Bemerkung möchte ich noch anbringen. Consideo, wie auch alle anderen Simulationswerkzeuge, besitzen Standardfunktionen für Verzögerungen in Material- und Informationsströmen. Das sind im CONSIDEO MODELER die Funktionen

• DELAY1 für eine Materialverzögerung 1. Ordnung
• DELAY3 für eine Materialverzögerung 3. Ordnung
• SMOOTH1 für eine Informationsverzögerung 1. Ordnung
• SMOOTH3 für eine Informationsverzögerung 3. Ordnung

Das Verwenden dieser Funktionen vereinfacht zwar das Erstellen des Modells, erschwert aber das spätere Verständnis, da der Prozess zwischen Input und Output nicht zu erkennen ist. Gerade bei Verzögerungen höherer Ordnung ist das absolut hinderlich, weshalb ich von dem Gebrauch dieser Funktionen abrate. Ich habe das Modell Bugfixing 3. Ordnung mit Funktionen modelliert. Dieses Modell finden Sie am Submodell “Funktionen”.

Fazit

Ein Verständnis von System Dynamics hilft Verzögerungen griffig zu machen, was wiederum unerlässlich ist, getätigte Aktionen auf Erfolg und Misserfolg zu evaluieren. Ich kann Ihnen kein Beispiel aus der Praxis nennen, wo keine Verzögerungen auftreten, sprich wo sofort eine Reaktion auf eine Aktion folgt. Alle Entscheider von heute sollten dementsprechend ein gesundes Verständnis für die quantitative Modellierung, beispielsweise System Dynamics, mitbringen.

(Keine Bewertungen bislang. Geben Sie doch die erste ab.)

Loading...