Eine der größten Errungenschaften der Mathematik ist sicherlich, dass Zahlen erfunden wurden, die als Basis für eine Sprache dienten, mit Hilfe derer man in der Lage war, Situationen und Thematiken so darzustellen und zu beschreiben, dass sie länder- und kulturübergeifend verständlich waren. Die mathematische Sprache hat also abstrahiert um zu vereinheitlichen. Diese Abstraktion, die ohne Frage wichtig ist, birgt allerdings auch Fallen, denen man sich bewusst sein muss, um nicht in diese zu tappen. Eine Falle besteht in dem Ignorieren von Qualitäten beim Verwenden von Zahlen im herkömmlichen Sinne. Bewusst ist mir dieser Fakt wieder geworden, als ich mit meiner Tochter, die derzeit die erste Klasse besucht, Rechnen geübt habe. Wenn wir den Kindern den Gedankengang beim Rechnen von Aufgaben wie 13+5 erklären wollen, benutzen wir häufig Objekte wie Stäbchen oder Murmeln (13 Murmeln und 5 Murmeln sind gleich 18 Murmeln). Das Wort gleich drückt aber eine Form der Qualität aus, denn es hängt davon ab von welchem Standpunkt diese Aussage getätigt wird. Diesen Fakt unterdrücken wir komplett, denn wir setzen alle Murmeln als gleich an. Durch die Einführung und Nutzung der Zahlen in der Mathematik, sind wir es also gewohnt exklusiv quantitativ zu denken.
Dieser Fakt ist aus meiner Sicht auch dafür verantwortlich, warum ganz häufig unangemessen mit komplexen Situationen in der Praxis umgegangen wird. Komplexe Situationen werden nämlich zu sehr trivialisiert, in dem Sie durch Algorithmen und den dazugehörigen Zahlen zu arg abstrahiert werden, so dass am Ende ein Modell entsteht, welches nicht mehr mit der wahrgenommenen Situation der Umwelt übereinstimmt. Damit werden dann auch alle Ergebnisse dieses Modells unbrauchbar. Um diese These zu belegen, möchte ich einen kleinen Exkurs in die Entstehung der Zahlen und ihre Kategorisierung wagen, bevor ich eine Gegenüberstellung von Zahlen mit Problemsituationen darlege. Mit dieser Gegenüberstellung möchte ich aufzeigen, warum komplexe Situationen, die uns heutzutage so viel Kopfzerbrechen bereiten, mit den herkömmlichen in allen Bildungseinrichtungen gelehrten Zahlen nicht handhabbar und dementsprechend auch nicht modellier- und lösbar sind.
Angefangen hat alles mit den natürlichen Zahlen. Kleinere Zahlen wie 1, 2, 3, … waren noch relativ einfach auszudrücken, in dem man Gegenstände dafür legte oder seine Finger benutzte. Problematischer wurde es dann bei größeren natürlichen Zahlen. Für das Ausdrücken wurden die großen natürlichen Zahlen zu Gruppen zusammengefasst, beispielsweise waren dies Zwölfer- und Sechzigereinheiten. Relikte aus dieser Zeit erkennen wir noch heute an den Zeit- und Winkelmessungen. Allerdings war das Rechnen mit diesen großen natürlichen Zahlen auch in diesen Gruppierungen schier unmöglich. Dafür wurden dann die Stellenwertsysteme erfunden. Gut bekannt ist das System zur Basis 10 (Dezimalsystem), mit welchem bereits die Kinder ab der ersten Klasse aufwachsen. Es gibt aber auch noch die Systeme zur Basis 2 (Dualsystem) und zur Basis 16 (Hexadezimalsystem). Bleiben wir kurz bei dem Dezimalsystem. Die Zahl 2145 in Dezimalschreibweise lautet 2*10^3+1*10^2+4*10^1+5*10^0. Der große Vorteil eines Stellenwertsystems ist, dass selbst die kompliziertesten Zahlenrechnungen auf das kleine Einmaleins zurückgeführt werden können, was dadurch dann selbst für die Schüler der unteren Schulklassen relativ schnell anwendbar wird. Wie wir allerdings wissen, sind nicht alle praktischen Probleme mithilfe natürlicher Zahlen beschreib- und lösbar. Die natürlichen Zahlen müssen also erweitert werden, in erster Instanz durch negative Zahlen, um beispielsweise die Gleichung 8+x=1 zu lösen. Es brauchte allerdings relativ lange, bis negative Zahlen Anerkennung fanden. Im 17. Jahrhundert waren sie teilweise noch verpöhnt. Diese Anerkennung wurde allerdings durch die fortschreitende Anwendung der Mathematik in der Finanzwirtschaft (Schulden) forciert. Die natürlichen zusammen mit den negativen Zahlen machen die ganzen Zahlen aus. Wann immer man Gleichungen der Art a+x=b zu lösen hat, in denen a und b exklusiv ganze Zahlen sind, muss man den Raum der ganzen Zahlen nicht verlassen. Anders sieht es bei den Punktoperationen aus. Nicht alle Gleichungen der Art a*x=b sind ausschließlich im Raum der ganzen Zahlen darstellbar, auch wenn a und b ganze Zahlen sind. Beispiele finden Sie sicherlich recht schnell. So kommen wir also zur nächsten Zahlenklasse, den rationalen Zahlen, die man auch als Brüche darstellen kann. Wenn wir ein bisschen mit den zu lösenden Gleichungen herumspielen, erkennen wir sehr schnell, dass auch die Brüche nicht ausreichen, um alle Gleichungen nur bis einschließlich den rationalen Zahlen darzustellen. Die Gleichung x*x=2 ist beispielsweise im Raum der rationalen Zahlen nicht lösbar. So gelangen wir zu den irrationalen Zahlen. Rationale und irrationale Zahlen spannen zusammen den Raum der reellen Zahlen auf.
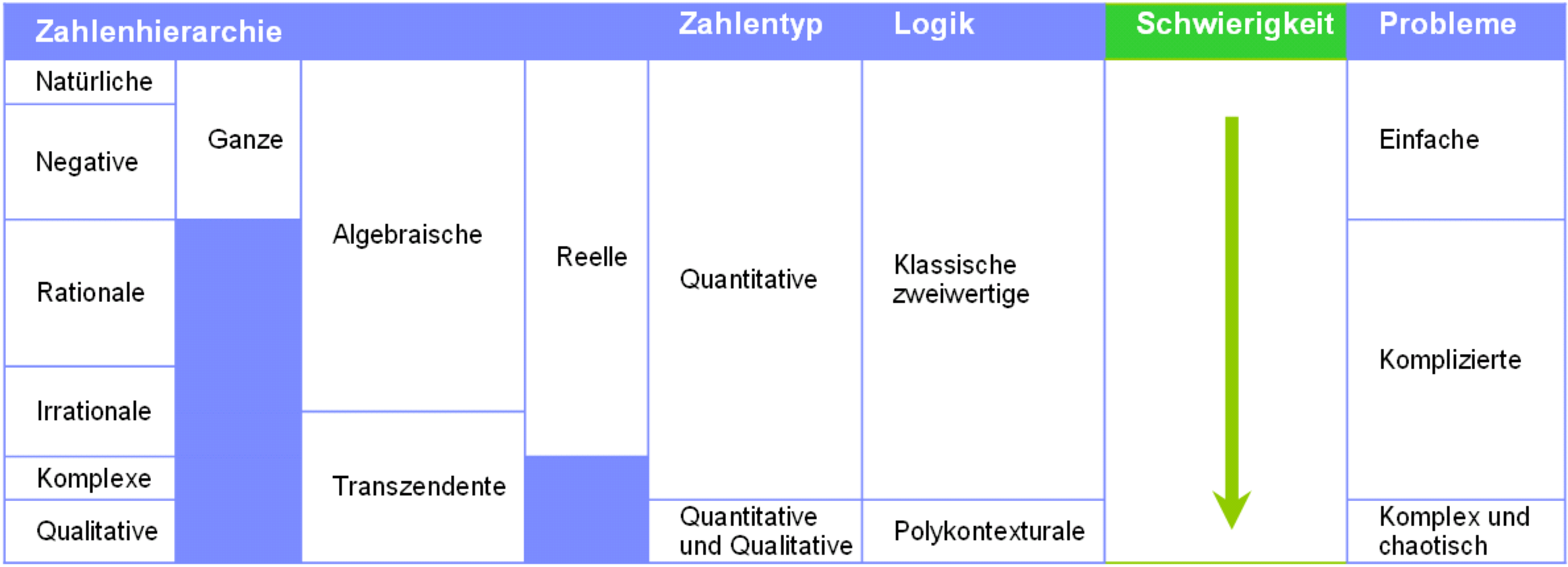
Halten wir kurz inne und verbleiben bei den reellen Zahlen. Die derzeit angeführten Zahlenklassen werden in dieser Reihenfolge wie ich sie kurz eingeführt habe, auch in den Schulen den Kindern beigebracht. Das hat einen guten Grund, nämlich der Schwierigkeitsgrad. Natürliche Zahlen sind einfacher als ganze Zahlen, diese sind einfacher als rationale und diese wiederum einfacher als irrationale. Bei den irrationalen Zahlen unterscheidet man aber ebenfalls noch nach dem Schwierigkeitsgrad. Es gibt also einfache und schwierige irrationale Zahlen. Um den Schwierigkeitsgrad von Zahlen zu evaluieren, kann man ein kleines Rechenspiel durchführen: Spieler 1 nennt seinem Gegenspieler 2 eine Zahl x. Der Gegenspieler 2 muss aus dem x und unter Verwendung natürlicher Zahlen und der Operationen +, – und * eine Null erzeugen. Eine Zahl x heißt algebraisch, wenn dem Spieler 2 dies gelingt und transzendent, wenn dies nicht gelingt. Die Wurzel aus 3 ist irrational und algebraisch, denn x*x-3=0. Für die Kreiszahl Pi, die ebenfalls irrational ist, lässt sich dieses Spiel beispielsweise nicht gewinnen. Deshalb ist Pi transzendent und schwieriger als die Wurzel aus 3.
Reichen nun die reellen Zahlen aus, um alle praktischen Probleme zu lösen? Noch aus der Schulzeit wissend kennen wir die Antwort. Nein. Mit den reellen Zahlen kann man beispielsweise die Gleichung x*x=-1 nicht darstellen. Wir kommen also zu den komplexen Zahlen. Komplexe Zahlen entstehen, wenn man zu den reellen Zahlen die Wurzel aus -1 zufügt. Schaut man sich aber die reellen Zahlen auf einer Linie aufgespannt an, dann erkennt man keine Lücke. Zwischen zwei beliebigen reellen Zahlen existieren wieder reelle Zahlen. Die komplexen Zahlen haben also auf dieser Linie keinen Platz mehr. Carl Friedrich Gauß war Anfang des 19. Jahrhunderts der erste, der die Frage formulierte, warum denn alle Zahlen auf einer Linie aufgereiht sein müssen. In einem zweidimensionalen Koordinatensystem bedeutet dies, dass die x-Achse alle reellen Zahlen darstellt und durch Zunahme der y-Achse, die den imaginären Bereich darstellt, die komplexen Zahlen gebildet werden. Auf der y-Achse wird also der eingebildete Teil dargestellt, mit i als Imaginärteil. Wird hier vielleicht die Integration zwischen Geist und Materie dargestellt? Ich habe dazu nichts in der Literatur gefunden, kann es mir aber gut vorstellen.
Bevor ich den Zusammenhang zwischen komplexen Zahlen und komplexen Sachverhalten aus meiner Sicht noch weiter ausführe, möchte ich ganz kurz auf Komplexität eingehen. Die Einteilung von Systemen nach ihren Charakteristika und den abgeleiteten Handlungsmotiven erkennen Sie in der folgenden Graphik.
Dave Snowden, von dem dieses so genannte Cynefin-Modell stammt, hat eine wie ich finde sehr geniale Einteilung der Systeme abgeleitet, die es uns erlaubt, verschiedene Typen von Systemen zu unterscheiden und dafür passende Entscheidungen für das Agieren in ihnen zu treffen. Details und weiteren Ausführungen finden Sie hier.
Komplexe Zahlen spannen also eine zweidimensionale Ebene auf. Die Menschen geben ihre Wahrnehmungen von der Umwelt ebenfalls zweidimensional wieder, in dem Sie Bilder malen. Erst mit den komplexen Zahlen ist es also überhaupt möglich, Begriffe mit Zahlen auszudrücken. Allein schon bei der begrifflichen Übereinstimmung von komplexen Zahlen und komplexen Problemen erkennt man die Überzeugung, denen die Menschen immer noch aufgesessen sind, das man mit Zahlen, die auf die klassische Aristotelische Logik fußen, komplexe Probleme handhaben kann, in dem man auf diese direkt einwirken, sie direkt steuern und managen kann. Das ist aber nicht der Fall, was wir wohl alle ganz deutlich an der Weltwirtschaftskrise gespürt haben. Denn was passiert auch bei den komplexen Zahlen nicht? Diese Zahlen bilden nur Quantitäten ab, keine Qualitäten. Subjektivitäten der einzelnen Beobachter und Beurteiler eines komplexen Sachverhalts können über komplexe Zahlen nicht abgebildet werden. Um dieses zu tun, muss man sich auf Gotthard Guenther berufen, der die qualitativen Zahlen erfunden hat inlusive der dazugehörigen Polykontexturalen Logik. Bemühen wir noch einmal die Metapher des Malen eines Bildes, um ein Problem zu beschreiben. Mehrere Beobachter einer Situation malen in der Regel verschiedene Bilder. Diese verschiedenen Bilder müssen aber eben auch in Zahlen darstellbar sein. Die komplexen Zahlen können das nicht. Das ist auch der Grund, warum in den Naturwissenschaften Subjektivitäten komplett ausgeschlossen sind. Oder haben Sie schon einmal von einem Experiment in der Physik oder Chemie gehört, in welchem die Subjektivtät des Experimentators Einklang gefunden hat? Es geht stets um objektive Erkenntnis von Subjekten.
Es werden in allen Bildungseinrichtungen die Zahlen immer nur bis zu den komplexen behandelt. Das gekoppelt mit dem Anspruch, alle Sachverhalte der Natur und Gesellschaft mechanistisch beherrschen zu wollen, lässt den Irrglauben der Menschen sich etablieren, dass die komplexen Zahlen ausreichend sind, um komplexe Sachverhalte zu beschreiben. Wir stehen also noch vor der gleichen Fragestellung vor der Plato seiner Zeit stand. Er war als Erster der Meinung, dass man Gegenstände und Objekte in Zahlen ausdrücken können müsste. Er kannte aber damals die komplexen Zahlen noch nicht und scheiterte daran. Das war der Grund, weshalb die komplexen Zahlen erfunden wurden. Wir sind aber trotzdem noch nicht viel weiter als Plato damals. Denn, die Zahlen, die eine subjektive Beschreibung komplexer Sachverhalte erlauben würden, nämlich die qualitativen Zahlen, werden von dem Maintream der Wissenschaften totgeschwiegen und Gotthard Guenthers Arbeiten als Scharlatanerie abgetan. Eine sehr gute Einführung zu den qualitativen Zahlen finden Sie in der Geschichte Morgen und Morgen von Claus Baldus.
Fazit: Die im Titel gestellte Frage ist aus meiner Sicht mit ja zu beantworten, obwohl ich betonen möchte, dass zwischen Zahlenverständnis und Problemhandhabung keine eineindeutige Beziehung besteht, was bedeutet, dass auch wenn wir die qualitativen Zahlen in unsere Mathematik einfließen lassen, so wie Gotthard Guenther es propagiert, es noch keine Garantie für das Handhaben von komplexen und chaotischen Problemen gibt. Es ist lediglich die Basis dafür.



Der BlaBlaMeter. Unglaublich, wie wir Menschen unsere Wirklichkeit mit Zahlen konstruieren, die dann der Realität so dermaßen nicht Stand halten kann. Die philosophisch-konstruktivistischen Diskussionen über die Unterscheidung von Realität und Wirklichkeit möchte ich hier mal umgehen. Die Effekte sehen wir tagtäglich in allen Bereichen: Politik, Wirtschaft etc. Wir müssen alles in Zahlen ausdrücken können, dann sind wir beruhigt. Und das wo unser Verständnis lange nicht ausreicht, um unsere Welt mit Zahlen auszudrücken. Spaßig ist es trotzdem, man sollte es nur nicht ernst nehmen.
Ein verrücktes Tagebuch. Unglaublich, wie du deine Gedanken in Worte fassen kannst. Eine tolle Schreibe! Liebe Grüße
Es gibt doch auch qualitative Eigenschaften der Zahlen. Schon nur die Bezeichnungen “ganz”, “rational”, “irrational”, “transzendent” unterscheiden ja Qualitäten, nicht Quantitäten. Und obwohl die alephs zwar mit der Mächtigkeit eine quantitative Charakterisierung einbringen, ist es doch eine qualitätive Eigenschaft, ob eine Zahlenmenge abzählbar oder überabzählbar ist.
Ich nehme die Mathematik mehr qualitativ als quantitativ wahr und bemühe mich, in meinen Vorlesungen den Leuten klar zu machen, dass Mathematiker nicht Rechenkünstler seien. Rechnen überlassen wir den Buchhaltern. Mathematik hat mit Strukturen, Mustern und Ästhetik zu tun, alles qualitative Dinge. Die Knotentheorie versucht zu bestimmen, wann zwei Knoten homöomorph sind. Ein Buch über Knotentheorie enthält viele Bildchen verschiedenster Knoten, auch unmögliche, hoch komplizierte. Oder betrachte die Theorie der Parkette. Wie schön sind doch Escher oder Penrose Parkette. Reine Asthetik, viel Qualität. Quantität ist nur im Hintergrund, um überhaupt darüber reden zu können.
Sie fragen: “Oder haben Sie schon einmal von einem Experiment in der Physik oder Chemie gehört, in welchem die Subjektivtät des Experimentators Einklang gefunden hat?”. Ich meine, dass das genau der Kern der Quantentheorie und der Quantenlogik ist. Der Experimentator wird in das System mit einbezogen. Sicher ist die QT noch insofern klassisch, als dass die Zeit umkehrbar ist. Aber die Subjektivität ist dort doch sehr zentral, und die Quantenlogik nicht aristotelisch. Ist doch schon mal etwas!
Hallo Peter,
mit Qualitäten meine ich etwas anderes. Das habe ich wohl nicht eindeutig genug ausgeführt, will es jetzt also nachholen.
Nehmen wir den Begriff der Zahl in der Mathematik. Die Zahl ist ein Maß für die Vielheit. Eine Zahl kennt nicht den Unterschied zwischen Gestaltgleichheit und -vielheit. Es werden stets gleiche Gestalten gezählt. Werden unterschiedliche Gestalten gezählt, dann werden die Unterschiede ignoriert. Zählt man 3 Äpfel und 4 Birnen zusammen, kommt man lediglich auf 7 Obststücke. Der Unterschied zwischen Apfel und Birne wird also trivialisiert auf Obst.
Diese Problematik lösen die qualitativen Zahlen, wie sie Gotthard Günther eingeführt hat. Er unterscheidet 3 Arten: Protozahlen, Deuterozahlen und Tritozahlen. Wie oben angedeutet halten Zahlen lediglich fest wieviel Dinge da sind. Protozahlen betrachten darüber hinaus wieviel verschiedene Arten von Dingen da sind. Deuterozahlen haben im Fokus wieviel Dinge von jeder Art von Dingen da sind. Tritozahlen ordnen darüber hinaus die teils gleichen und teils verschiedenen Dinge in einer Reihe an. Diese Arten von qualitativen Zahlen werden in der oben von mir angesprochenen Geschichte Morgen und Morgen von Claus Baldus als Zahlrot, Zahlgelb und Zahlblau ab Seite 22 eingeführt.
Um diese Zahlen allerdings einführen zu können, musste Günther einen kleinen Umweg gehen, in dem er Leerzeichen, so genannte Kenogramme, in seine Theorie aufnahm. Was ist aber der Unterschied zwischen Ding und Leerzeichen? Für Dinge, die gegeben sind, ist bereits entschieden, ob diese gleich oder verschieden sind, für Leerzeichen nicht. Leerzeichen können erst in dem Moment verglichen werden, wenn sie mit einer der oben angesprochen qualitativen Zahlen interagieren. Die Frage nach Verschieden- oder Gleichheit von Leerzeichen kann also ausschließlich gleichzeitig mit einer Operation wie die Addition beantwortet werden. Die Leerzeichen haben keine eigenständige autonome Bedeutung. Wir erhalten also ein Modell für verteilte Subjektivitäten. Die Entscheidung ereignet sich zwischen den Leerzeichen, wenn sie sich additiv zusammentun oder wenn sie subtraktiv auseinandergehen.
Warum meine ich nun, das mit dem Verständnis für die qualitativen Zahlen auch die Fähigkeit für das Handhaben von Komplexität gesteigert wird? Mit der Einbeziehung von qualitativen Zahlen sind wir in der Lage Strukturen und Prozesse offen zu legen, die durch die Trivialisierung auf Gleichheit bei Verwendung von herkömmlichen Zahlen, verborgen bleiben. Das auf die Kommunikation umgemünzt, bedeutet, dass wir die Bedeutung von Wörtern nicht als abstrakt identisch, also objektiv ansehen, sondern als subjektiv. Und darauf kommt es letztlich an, wenn wir lebendige Prozesse formallogisch darstellen und modellieren wollen. Denn, um es anders auszudrücken, unser Denken ist auf dem Identitätsprinzip ausgelegt, was uns aber nicht hilft, komplexe Probleme zu durchdringen. Wir sind den Paradigmen unseres Denkens erlegen und können nicht aus denen heraustreten.
Das Problem, mit Zahlen Komplexität “berechenbar” zu machen:
Stellenwert und Aussagekraft von Zahlen beruhen immer auf ihrer Verhältnismäßigkeit zu anderen Zahlen bzw. auf dem Charakter der Formeln in denen sie Anwendung finden.
Das bedeutet im Klartext:
Jede Berechnung, egal mit welcher Art Zahlen (quantitativ und/oder qualitativ), ist nur so gut und zutreffend brauchbar, wie die Formel in ihrer Grundstruktur tatsächlich imstande ist, reale Verhältnismässigkeiten zu berücksichtigen und formell darzustellen.
Das Problem mit Formeln:
Jede Formel steht für sich und bildet einen definierten Ausschnitt der Realität ab.
Wenn Du ein Flugzeug baust, benötigst Du die serielle Abarbeitung von unterschiedlichen Formeln in verschiedensten Bereichen.
Beim Flugzeug funktioniert das, weil das Endprodukt invariabel ist und die Prozeßschritte der Herstellung prinzipiell unabhängig von anderen statt finden können.
Wenn das Flugzeug dann von A nach B fliegen soll, ist dies formell gesehen ein einfacher prozeßtechnischer Akt, der mathematisch leicht erfasst, berechnet und in Routendaten umgesetzt werden kann.
Wenn dann aber das Chaos (Non-Linearität) in Form eines Unwetters, eines magnetischen Sturms oder systemimmanenten Friktionen/Emergenzen über das Flugzeug (Lineares System mit linearen Handlungsroutinen) hereinbricht, dann versagt jegliche Mathematik insofern, als weder ausreichend Daten noch Zeit zu deren Berechnung zur Verfügung stehen, um Systemstabilität herzustellen und zu erhalten.
Das Flugzeug steuert dann nicht mehr klassische oder quantenmechanische Mathematik, sondern ein Pilot, der seine “Berechnungen” der zur Stabilisierung des Systems notwendigen Aktionen auf ganz anderer Basis vollzieht.
Das Flugzeug stürzt dann nicht ab, wenn es dem Piloten gelingt, die zur Systemstabilität erforderlichen Kompensationsleistungen zu erbringen- andernfalls schmiert er ab.
Die Kompensationsleistung ist die Schlüsselfunktion, die sich mathematisch nicht erfassen oder beschreiben lässt, da es unmöglich ist, vierdimensionale Vektorenkonglomerate in beliebiger Anzahl zu berechnen.
Die Kompensationsleistung des Piloten besteht im Abgleichen des künstlichen Horizonts (also eines Referenzsystems) mit der aktuellen Lage des Flugzeugs.
Dazu muss er zwei Komponenten korrekt kombinieren, nämlich die biaxiale Ruderführung und Geschwindigkeit.
Dass die Bewältigung einer so komplexen Situation, wie die Stabilisierung eines Flugzeugs unter chaotischen Bedingungen mit lediglich 3 Grundparametern (Höhe, Richtung, Geschwindigkeit) überhaupt funktioniert, zeigt, dass die Bewältigung von Komplexität nicht einer neuen Generation von Zahlen bedarf, sondern der Ermittlung der entscheidenden Grundparameter und deren korrekte Relationierung geschuldet ist.
Die Relationierung ist aber keine mathematische im klassischen Sinne, sondern eine Orientierung an ausschließlich gefühlsgesteuerten Verhältnismäßigkeiten.
Diese sind wiederum absolut ausschließlich von der jeweiligen Disposition des Piloten abhängig (Alter mit Erfahrung, Reaktionsgeschwindigkeit, Gelassenheit, “Gespür” für “sein” Flugzeug, Trainingsverfassung u.ä.).
Selbst wenn ich alle chemischen Moleküle, ihren Zustand und ihre Verbindungstendenz etc. quantitativ und qualitativ datenmaximal erfasse und formell korrekt berechne, inklusive neuronaler Repräsentanzen usw. werde ich als Neurophysiologe und Biochemiker niemals vorhersagen können, noch nicht mal Sekunden vorher, ob der Proband sich jetzt gleich verlieben wird oder nicht.
Es gibt also offensichtlich reale Instanzen, die NICHT mathematisch erfassbar sind, nicht , weil das notwendige System fehlt, sondern weil das mathematische System insgesamt nicht dazu geeignet ist, EMERGENZEN zu berücksichtigen!
Die Natur der Emergenz ist es ja definitionsgemäss und nachgerade eben NICHT berechenbar zu sein, sonst wäre es ja keine.
Wenn Du ein Pferd reitest, dann niemals auf mathematischer Basis, da das Pferd ein permanenter Emergenzreaktor ist.
Kontrolle über das System Pferd ist nur möglich über grundsätzliche Gesamtstabilisierung durch vorauseilende Kompensationsleistungen in Form der Erstellung und Erhaltung idealer Systemgrundbedingungen, dann durch hypersensible Wahrnehmung bezüglich Abweichungen von der Gesamtstabilität im kleinsten Bereich und ebenfalls direkt entsprechender Kompensationsleistung und traumwandlerischer Reaktionssicherheit in den dazu nötigen Handlungsoptionen.
Wenn der Reiter reagiert, kommt er immer zu spät.
Der Reiter muss konsequent proaktiv tätig sein.
Der gute Pilot macht es übrigens genau so, – der “reitet” nämlich den Sturm aus^^
Die Variablengemengelage in echten komplexen Situationen erfordert also kein mathematisches System, sondern immer Kompensationsleistungen unter emergentem Vorzeichen – soll heißen:
Improvisationsleistung, die auf einer radikal schnellen Permutationsrate möglichst vieler situationsadäquater Faktoren (das wäre in der Tat mathematisch möglich, wie beim Schachcomputer) und der gefühlsmässigen Gewichtung in Abgleich zu einer internen erfahrungsbasierten Zielvorstellung beruht!
Und dass es dafür keine Mathematik geben kann, ist selbsterklärend^^
Was es “mathematisch” geben kann ist allerdings die Formulierung von Algorithmen, die den Improvisationsvorgang initiieren und aufrecht erhalten helfen.
Mehr aber auch nicht.
Ergänzung:
Sollte es dereinst ein Meßsystem für diese Qualitäten geben und ein Computersystem, welches paradoxe Berechnungen (in komplexen Systemen treten schon mal paradoxe Bedingungen auf – was gerade eben noch richtig war, ist im nächsten Moment falsch – und es gibt noch keine Mathematik, die diesen Widerspruch formell zu lösen imstande ist, weil 2+2=4 im selben Bezugssystem nicht mal eben richtig und eben falsch sein kann!) durchführen kann, dann besteht Hoffnung.^^
Hi Nick,
danke für das super Feedback.
Das wir niemals die Zukunft vorhersagen können, ist uns glaube ich allen, oder sagen wir lieber fast allen, bewusst. Das meine ich auch nicht, wenn ich davon spreche, dass wir ein neues Verständnis von Zahlen oder auch eine neue Art von Zahlen benötigen, um Komplexität besser handhaben zu können. Ich spreche mit Absicht nicht davon, dass wir Komplexität beherrschen können. Das werden wir niemals können, denn in dem wir eine Situation analysieren, fokussieren wir uns auf die von uns ausgewählten und wahr genommenen Variablen. Damit nehmen wir diese aus den Gesamtzusammenhang und zerstören die Ausgangslage. Das bedeutet, unsere Wahrnehmung und damit unser Umgang mit Komplexität ist stets subjektiv. Sie hängt von unserer Fähigkeit der Wahrnehmung ab und von den in der Vergangenheit von uns gemachten Erfahrungen und die daraus in uns aufgebauten “inneren Bildern” und unserem Wissen.
Und nun kommen wir zum Kern: die Subjektivitäten. Die heutige Mathematik kann diese nicht abbilden, da das Gesetz der Identität fest in ihr verankert ist. Wie Du in Deiner Ergänzung richtig ausführst, stoßen wir bei Nichtbeachtung der Existenz der Identität auf Paradoxien, die die heutige Mahtemtik nicht handhaben kann. Das hat Gotthard Günther mit seiner Polykontexturalitätstheorie und den dazu gehörigen Kenozahlen aufgebrochen. Allerdings sind die Erkenntnisse beispielsweise noch nicht in den Bereich der KI vorgedrungen. Deshalb wird es auch, und da gebe ich Dir Recht, mit der heute vorherrschenden Mathematik unmöglich sein, intelligente Maschinen zu bauen. Das ist vielleicht auch gut so.
Hast Du die Geschichte von Claus Baldus, die ich oben angeführt habe, gelesen? Hier wird die Notwendigkeit quantitative Zahlen zu haben, um Komplexität besser verstehen und handhaben zu können, wie ich finde sehr gut dargestellt.
Gotthard Günther formuliert in seiner Selbstdarstellung auf der Seite 41 sehr eindrucksvoll die Notwendigkeit von qualitativen Zahlen in der Mathematik, um Subjektivitäten formallogisch abzubilden, was überhaupt erst die Basis für die technische Umsetzung Künstlicher Intelligenz ist.
Die Wissenschaftler des heutigen Mainstream würden diese Frage auch heute noch als Unsinn abtun, weil sie die Wichtigkeit dieser Frage nicht erkennen. Wenn Sie dies nämlich tun würden, würden Sie Folgendes antworten, was ebenfalls auf der Seite 41 einzusehen ist.
Mit diesem Gedanken würden Sie die Misere der heutigen Wissenschaft, die auf der zweiwertigen Logik aufgebaut ist, erkennen und nach einer Lösung suchen. Übrigens ist die Lösung bzgl. der qualitativen Zahlen, wie schon mehrfach erwähnt, inklusive der Rechenregeln, der Polykontexturalitätstheorie, von Gotthard Günther bereits dargelegt und veröffentlicht. Es will nur Niemand sehen, da das Problem noch gar nicht erkannt ist.
Wir sind also noch sehr weit davon entfernt, irgendwann einmal intelligente Roboter in unseren Reihen begrüßen zu können.
Pingback: Kommunikation ist Er-, Be-, Ver- und Entsetzung | Reise des Verstehens