Ich möchte mit diesem Beitrag nicht in die Hysteriehörner rund um Corona blasen, sondern mittels eines kleinen mathematischen Modells die Ausbreitung der Viren erklärbarer machen. Letztendlich geht es um exponentielles Wachstum, welches für uns Menschen eher kontraintuitiv ist, da wir uns oft nicht vorstellen können, wie schnell sich eine Krankheit ausbreiten kann.
Das kleine mathematische Modell hat 2 Inputfaktoren. Diese Faktoren können wir Menschen beeinflussen.
- Der erste Faktor, im Modell mit der Variable a bezeichnet, ist die Anzahl der Menschen, die eine infizierte Person je Tag trifft.
- Der zweite Faktor b trägt die Wahrscheinlichkeit des Ansteckens bei einem Treffen einer infizierten und einer nicht infizierten Person.
Dann gibt es noch einen weiteren Faktor c, der die maximale Anzahl der Bevölkerung trägt. Wenn ich oben vom exponentiellen Wachstum gesprochen habe, dann muss ich mich hier korrigieren und vom logistischen Wachstum schreiben. Es gibt ja nicht unendlich viele Menschen auf der Erde, die sich anstecken könnten. Je mehr sich die Anzahl der infizierten Menschen dieser maximalen Anzahl annähert, desto weniger Menschen infizieren sich bei einem Treffen, was ja einsichtig ist, denn wenn sich 2 bereits infizierte Menschen treffen, gibt es keinen neuen infizierten Menschen, da beide bereits infiziert sind. Für diese eine Simulation setze ich den Faktor c auf 10.000.
Die folgende Abbildung enthält die Herleitung der Formel für den Bestand der infizierten Menschen je Tag.
Der Faktor (1-(Infiziertealt/c)), der in die Formel eingeschoben wurde, modelliert den oben beschriebenen Effekt, dass je mehr Menschen bereits infiziert sind, desto weniger Menschen sich bei einem Treffen infizieren können.
Für die Simulation habe ich die Wahrscheinlichkeit des Ansteckens bei einem Treffen einer infizierten und einer nicht infizierten Menschen auf 10% gesetzt. Das bedeutet in 1 von 10 Treffen wird ein nicht infizierter Menschen angesteckt, 9 bleiben nicht infiziert.
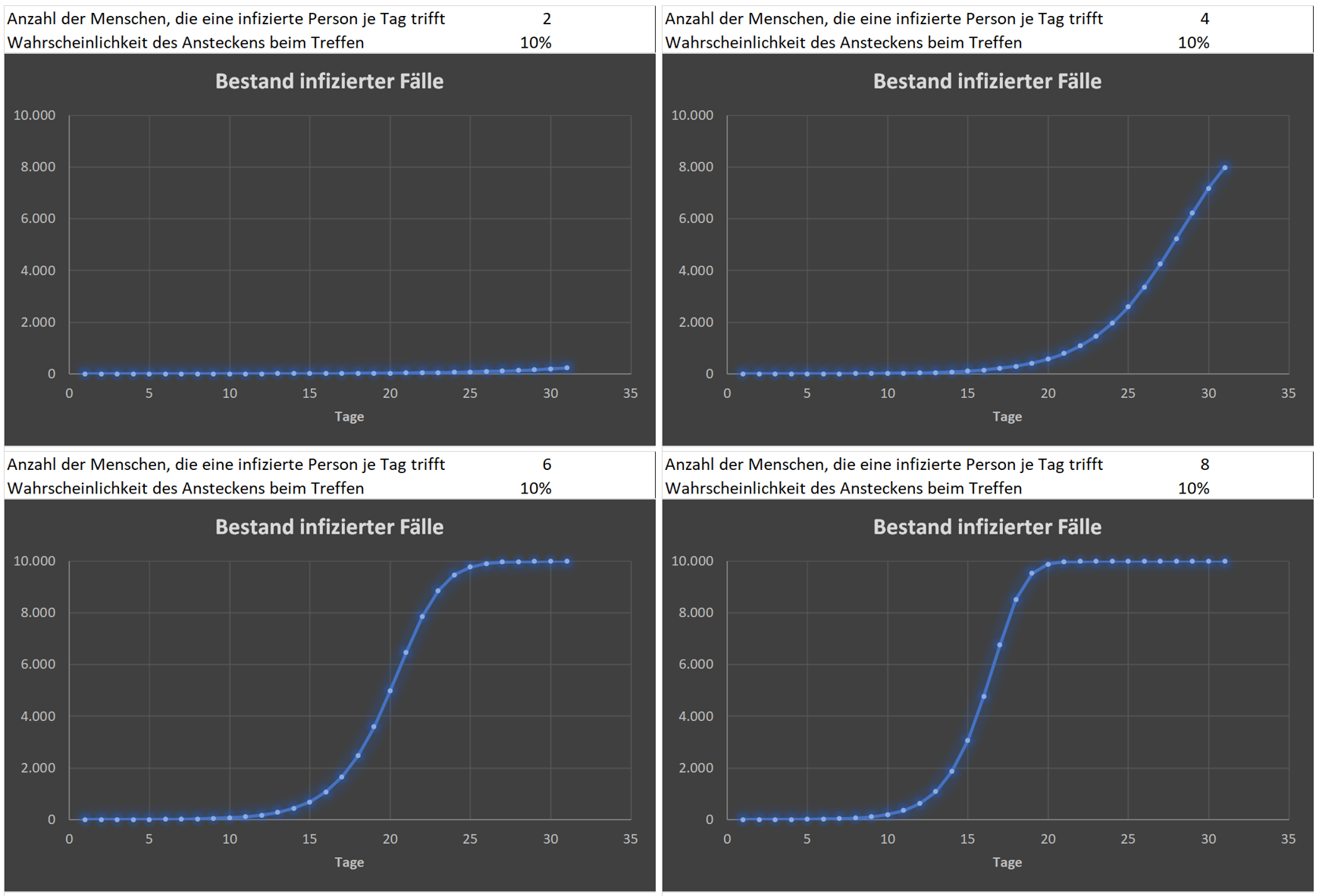
Die folgende Abbildung stellt 4 Simulationsergebnisse dar, bei denen ich einzig und allein die Anzahl der Menschen ändere, die eine infizierte Person je Tag trifft: 2, 4, 6 und 8.
Folgendes Ergebnis ist ersichtlich.
- Trifft ein infizierter Mensch bei einer Wahrscheinlichkeit von 10% der Ansteckung pro Tag 2 nicht infizierte Menschen sind nach einem Monat 233 Menschen infiziert.
- Trifft ein infizierter Mensch bei einer Wahrscheinlichkeit von 10% der Ansteckung pro Tag 4 nicht infizierte Menschen sind nach einem Monat 7.985 Menschen infiziert.
- Trifft ein infizierter Mensch bei einer Wahrscheinlichkeit von 10% der Ansteckung pro Tag 6 nicht infizierte Menschen sind nach einem Monat alle 10.000 Menschen infiziert.
- Trifft ein infizierter Mensch bei einer Wahrscheinlichkeit von 10% der Ansteckung pro Tag 8 nicht infizierte Menschen sind bereits nach 24 Tagen alle 10.000 Menschen infiziert.
Jetzt erkennen Sie sicher die Kontraintuitivität. Ein kleines Ändern der Anzahl der nicht infizierten Menschen, die ein infizierter Mensch pro Tag trifft, hat so enorme Auswirkungen in der Ausbreitung eines Virus.
Noch 2 Anmerkungen zum Schluss.
Es bleibt natürlich ein Modell und erklärt nur so viel, wie im Modell hinein modelliert wurde und das auch simplifiziert. Und diese hier modellierten Zusammenhänge sind nicht alleine auf die Corona-Epidemie zu beziehen, sondern auf alle Arten von Epidemien anwendbar. Es ist und bleibt stets unglaublich sinnvoll die Kontaktmöglichkeiten zwischen Menschen einzuschränken, um die Ausbreitung der Viren einzudämmen. Den Effekt erkennt man in der Simulation. Vorsicht im Umgang miteinander ist also stets geboten, ganz egal um welches Virus es sich handelt.
Welche Unterschiede nun zwischen dem Corona-Virus und anderen Viren der Epidemien und Pandimien der Vergangenheit bestehen, möchte ich hier gar nicht beleuchten, da ich auf diesem Gebiet kein Experte bin.
Falls Sie ebenfalls Interesse an einigen Simulationen haben, können Sie gerne das von mir erstellte Excel-Modell verwenden.



 (7 Bewertung(en), Durchschnitt: 4.71 von 5)
(7 Bewertung(en), Durchschnitt: 4.71 von 5)
Hier gibt es Zahlen..
https://www.heise.de/newsticker/meldung/Zahlen-bitte-3-4-Coronavirus-Fallsterblichkeit-False-Number-4679338.html
Jedoch stellt sich heraus, dass es auf die Datenbasis ankommt und es gar nicht so einfach ist. Mathematik braucht verlässliche Zahlen bzw. muß passend intepretiert werden.
Verlässliche Zahlen sind gut. Jedoch habe ich mit meinem Modell einen anderen Fokus angelegt. Mir ging es eher um das Muster des Wachstums. Die verwendeten Zahlen habe ich dann nur zum Simulieren genutzt, das Muster offen zu legen.
Hi Conny
Interessant ist die Möglichkeit der Dynamisierung und die Kombination mit anderen Parametern, wie etwa der Anzahl unbehandelter Fälle: https://www.know-why.net/model/CHFWUVddNJsog2quA15x0PQ
Dort ist in den Kommentaren auch ein Link auf eine Reihe von realen Daten vs. Modellen. In System Dynamics wird das btw. Bass-Diffusion genannt.
Happy modeling
kai
Moin Kai, danke für das Modell. Interessant. BG, Conny
Danke, lieber Conny. Du hast es so gut hergeleitet und beschrieben, dass es für mich gut verständlich und nachvollziehbar ist! Wir sind nun auch alle im HomeOffice, als ganze Firma und arbeiten unter Hochdruck daran, dass den Eltern das #HomeSchooling gelingt.
Danke für Deine Antwort Sana. Dann bleibt wohlauf im Homeoffice. LG, Conny
Vielen Dank für diese wertvolle Darstellung!
Ich finde Sie auch im umgekehrten Sinn sehr wichtig, weil auch folgendes kontraintuitiv ist: Ab wann bringen Maßnahmen nur mehr einen sehr geringen Effekt, um die Verbreitung einer Epidemie/Pandemie zu verhindern.
Anmerkung: Ich nehme zum leichteren Verständnis und weil es für meine Argumentation im unteren Bereich irrelevant ist raus, dass die Menschheit endlich ist. Ich habe die Zahlen auch in Excel gegossen, falls das jemand haben will.
z.B.: Verbreitung wenn nichts geschieht: 100% Wachstum = tägliche Verdoppelung
Start Sonntag Abend: 100=>200=>400=>800=>1600=>3200=>6400=>12800 (Sonntag Abend)
Faktor 1 Woche also: 128fach;
Anzahl nach 28 Tage damit 26 Mrd. also mehr als die Menschheit
Maßnahme A:
Wir appellieren an eine bereits sensibilisierte Gesellschaft: Nicht mehr Hände schütteln, Abstand, halten, Waschen, nicht anniesen …
Wirkung: Wirkung: 50% Reduktion = also z.B:
Start Sonntag Abend: 100 => 150 => 225=>337=>506=>759=>1139= 1709 (Sonntag Abend).
Faktor für 1 Woche: 17-fach
Anzahl nach 28 Tagen: 8,5 Millionen (ca. Österreichisches Bevölkerung)
Davon Schwererkrankte mit Krankenausbedarf (15% laut Statistik / Rest ist leichter Verlauf): 1,2 Mio
Maßnahme B:
Wir vermeiden zusätzlich 25% unserer normalen Sozialkontakte; Wirkung (lt. Österreichischem Gesundheitsminister 50% weniger Ansteckung) Übertragung damit statt 50% auf 25%;
Start Sonntagabend: 100 =>125 => 156=>195=>244=>305=>381=>477 (Sonntagabend)
Faktor für 1 Woche: 5-fach
Anzahl nach 28 Tagen: 51.699 (ca. eine Kleinstadt)
Davon Schwererkrankte mit Krankenausbedarf (15% laut Statistik / Rest ist leichter Verlauf): 7.700.
Anmerkung. In Österreich gibt es ca. 60.000 Krankenbetten / davon 2.500 Intensivbetten
Maßnahme C:
Wir verhindern zusätzlich große Veranstaltungen, Ansammlungen von Menschen (z.B. Konzert/Sport-Veranstaltungen; Schließen von Schulen)
Annahme fiktiv: (Ich habe keine Ahnung was das tatsächlich bringt) ich tippe mal auf zusätzlich 25%
Übertragung: Statt 25% damit 18,75%
Start Sonntagabend: 100 =>119 => 141=>167=>199=>236=>280=>333 (Sonntagabend)
Anzahl nach 28 Tagen: 12.300 (ca. eine Kleinstadt)
Davon Schwererkrankte mit Krankenausbedarf (15% laut Statistik / Rest ist leichter Verlauf): 1.844.
Maßnahme D:
Wir schließen Geschäfte (außer Lebensmittel etc.), Restaurants, Hotels, Skigebiete, etc.
Annahme Fiktiv (Ich habe keine Ahnung was das tatsächlich bringt) ich tippe mal auf zusätzlich 10%
Übertragung: Statt 25% damit 16,875%
Start Sonntagabend: 100 =>117 => 137=>160=>187=>218=>255=>298 (Sonntagabend)
Anzahl nach 28 Tagen: 7.874 (ca. ein größerer Ort)
Davon Schwererkrankte mit Krankenausbedarf (15% laut Statistik / Rest ist leichter Verlauf): 1.181
Maßnahme E:
Ich verfüge Ausgangsbeschränkungen, schränke die Reisefreiheit massiv ein, und lege weitere Teile der Wirtschaft still. (was in Österreich gestern geschehen ist)
Annahme fiktiv (Ich habe keine Ahnung was das tatsächlich bringt) nachdem das ja eine äußert massive Maßnahme ist.
Übertragung: Statt 16,875% damit 8,4375%
Start Sonntagabend: 100 =>108 => 118=>128=>138=>150=>163=>176 (Sonntagabend)
Anzahl nach 28 Tagen: 966 (ca. ein Dorf)
Davon Schwererkrankte mit Krankenausbedarf (15% laut Statistik / Rest ist leichter Verlauf): 145
In dieser Darstellung ist nicht enthalten, dass es ja für besonders gefährdete Personen (Ältere, Vorerkrankte) noch besondere Schutzvorkehrungen getroffen werden!
Die Frage ist also: Welche Maßnahmen sind absolut sinnvoll und wichtig, wo kann man überlegen, dass alternative Maßnahmen wirkungsvoller wären und wo schießt man vielleicht deutlich über das Ziel hinaus und richtet entsprechende Folgeschäden an.
Wow. Ganz lieben Dank für die Ergänzungen. Sehr anschaulich. BG, Conny
In Österreich bewahrheiten sich derzeit ca. die Zahlen der Prognose C durch Maßnahme von E. Die Zahl der gleichzeitig (identifizierten ) Erkrankten pendelt sich bei 10 – 20K ein (wahrscheinlich näher bei 10).
Zu Beginn der Krise wurde informiert, dass 300.0000 die kritische Größe für unser Gesundheitssystem ist (also Faktor 15-30). Ziel hätte also in jedem Fall die Szenario B sein müssen. Wir sind also so gesehen über das Ziel hinausgeschossen. (Derzeit gibt es keine derartigen Ziele. )
Fazit: Massive Maßnahmen sind absolut wichtig, überhaupt keine Diskussion. Z.B. Schulschließungen, Verbot von Veranstaltungen, Gastgewerbe etc. . “Normale” Distanzregeln (Kontaktmeidung, wenn notwendig Abstand halten, nach Möglichkeit absolut selbstverständlich. Genauso wie der Schutz von Risikogruppen udn Vorbeugende Maßnahmen für Kapazitäten im Gesundheitssystem.
Aber: Ultramassive Maßnahmen können aber enormen Schaden anrichten. Nicht nur wirtschaftlich, wohl gemerkt.
Z.B. Über mehr 500.000 isolierte Erwachsene über 75J, von denen viele verängstigt sind, keinen Arzt aufsuchen etc.) wird nicht gesprochen.
Mir Sicherheit hätten auch Massive Maßnahmen die Zeit gegeben, die Situation zu beobachten und immer noch zu reagieren, wenn die Werte zu stark steigen.
(Für Deutschland die Werte einfach * 10 nehmen – das kommt immer ganz gut hin)
Danke für Deine Ergänzungen, Walter. BG, Conny
https://www.youtube.com/watch?v=2hkpfR-J5os
Dieses Video veranschaulicht sehr gut deine Aussagen im Blog. Ev. über andere Kanäle verteilen. Die Botschaft und der mathematische Level sind im Grunde vergleichbar.
Oh cool. Danke für das Video, Walter. BG, Conny